
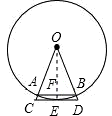
 解:如图所示,AB、CD分别是⊙O的内接正十边形与外切正十边形的一条边,设OA=r,连接OE,则OE⊥CD,由垂径定理可得OE⊥AB,
解:如图所示,AB、CD分别是⊙O的内接正十边形与外切正十边形的一条边,设OA=r,连接OE,则OE⊥CD,由垂径定理可得OE⊥AB, ×
× =18°,OF=OA•cos∠COE=r•cos18°,
=18°,OF=OA•cos∠COE=r•cos18°,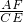 =
=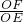 =
= =cos18°,
=cos18°,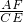 =cos18°.
=cos18°.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com