
 ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由.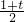 ,BH=
,BH= (t+1),
(t+1),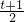 =
=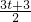 ,
,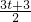 ,
, (t+1))(2分)
(t+1))(2分)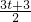 ,
, (t+1))代入直线OB的解析式y=kx,
(t+1))代入直线OB的解析式y=kx,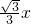 ,
,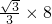
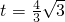 (3分)
(3分)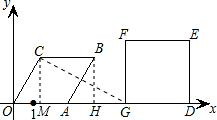
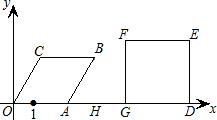
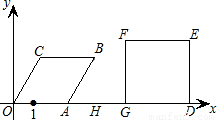
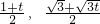 ),G(8-2t,0),D(8,0),
),G(8-2t,0),D(8,0),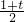 ,CM=
,CM=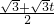 ,
,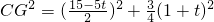 ,
,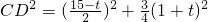 ,GD2=4t2
,GD2=4t2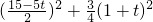 =
=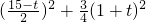 t1=0(舍去)t2=5
t1=0(舍去)t2=5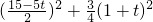 =4t2,
=4t2,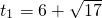 ,
,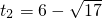 ,
,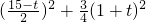 =4t2,
=4t2,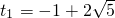 ,
,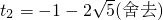 (11分)(每种情况2分)
(11分)(每种情况2分)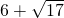 ,
,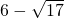 ,
,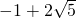 (12分)
(12分)

 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
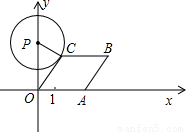
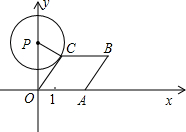 A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:
A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:查看答案和解析>>
科目:初中数学 来源: 题型:
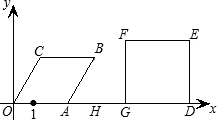 ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2010年江苏省无锡市惠山区八校联考中考适应性训练数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第26章《圆》中考题集(48):26.5 直线与圆的位置关系(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com