
 量x的取值范围.
量x的取值范围.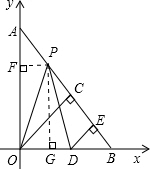 解:(1)作PG⊥x轴于点G,PF⊥y轴于点F,
解:(1)作PG⊥x轴于点G,PF⊥y轴于点F, AP,
AP, =
= AP,
AP, x (2分);
x (2分); -
- x,BE=
x,BE= BD=
BD= (10-x)=
(10-x)=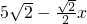 ,
, ,BE=
,BE= BD=
BD= (x-10)=
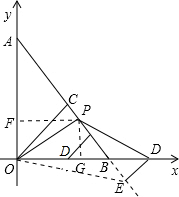
(x-10)= ,
,
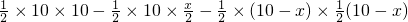 ,
, x2+
x2+ x+25,
x+25, x(10-
x(10- )+
)+ x•
x•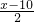 ,
, x.
x. .那么通过矩形FPGO的两对边FP=OG建立AP与OD间的联系.列出AP关于x的关系式.
.那么通过矩形FPGO的两对边FP=OG建立AP与OD间的联系.列出AP关于x的关系式.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
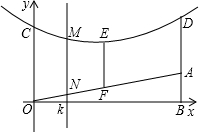 y轴,建立平面直角坐标系,已知OA=41米,AB=9米,OC=AD=10米,坡面中点F处与电线的距离EF=7.5米
y轴,建立平面直角坐标系,已知OA=41米,AB=9米,OC=AD=10米,坡面中点F处与电线的距离EF=7.5米查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
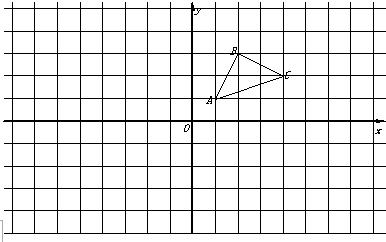
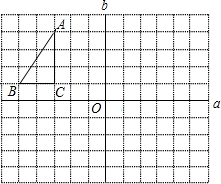 ,请写出△A″B″C″各顶点的坐标,并求出△A″B″C″的周长(结果用根号表示).
,请写出△A″B″C″各顶点的坐标,并求出△A″B″C″的周长(结果用根号表示).查看答案和解析>>
科目:初中数学 来源: 题型:
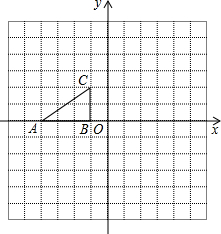 如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.
如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com