
如图,直线y=kx-2与x轴、y轴分别交于B、C两点,OB:OC=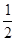 .
.
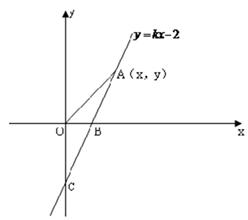
(1)求B点的坐标和k的值.
(2)若点A(x,y)是第一象限内的直线y=kx-2上的一个动点,当点A运动过程中,①试写出△AOB的面积S与x的函数关系式;②探索:当点A运动到什么位置时,△AOB的面积是1.③在②成立的情况下,x轴上是否存在一点P,使△POA是等腰三角形.若存在,请写出满足条件的所有P点的坐标;若不存在,请说明理由.
(1)B(1,0),k=2;
(2)①S=x-1,②(2,2),③存在,P1(2,0),P2(4,0),P3(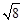 ,0),P4(-
,0),P4(-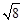 ,0).
,0).
【解析】
试题分析:(1)直线y=kx-2与x轴、y轴分别交于B、C两点坐标B( ,0)C(0,-2)又有OB:OC=
,0)C(0,-2)又有OB:OC=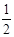 解得k=2求出B(1,0)
解得k=2求出B(1,0)
(2)△AOB的面积S与x的函数关系式是:S=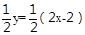 =x-1.
=x-1.
(3)①当s=x-1=1时 得x=2;x=2时y=2×2-2=2,所以,当A点坐标为(2,2),△AOB的面积是1
②存在.当OA=OP时,P点的坐标为(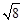 ,0), (-
,0), (-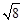 ,0);当OP=AP时,P点的坐标为P(2,0);当OA=AP时,P点的坐标为(4,0).所以,满足条件的所有P点的坐标为:P1(2,0),P2(4,0),P3(
,0);当OP=AP时,P点的坐标为P(2,0);当OA=AP时,P点的坐标为(4,0).所以,满足条件的所有P点的坐标为:P1(2,0),P2(4,0),P3(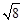 ,0),P4(-
,0),P4(-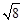 ,0).
,0).
试题解析:(1) 直线y=kx-2与x轴、y轴分别交于B、C两点坐标B( ,0)C(0,-2)
,0)C(0,-2)
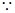 OB:OC=
OB:OC=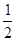
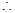 k=2
k=2
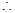 B(1,0)
B(1,0)
(2) ①△AOB的面积S与x的函数关系式是:S=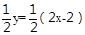 =x-1.
=x-1.
②当s=x-1=1时 得x=2;x=2时y=2×2-2=2,所以,当A点坐标为(2,2),△AOB的面积是1
(3)存在.当OA=OP时,P点的坐标为(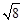 ,0), (-
,0), (-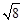 ,0);当OP=AP时,P点的坐标为P(2,0);当OA=AP时,P点的坐标为(4,0)所以,满足条件的所有P点的坐标为P1(2,0),P2(4,0),P3(
,0);当OP=AP时,P点的坐标为P(2,0);当OA=AP时,P点的坐标为(4,0)所以,满足条件的所有P点的坐标为P1(2,0),P2(4,0),P3(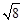 ,0),P4(-
,0),P4(-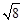 ,0).
,0).
考点:1.一次函数的图像和性质;2.动点问题;3.分类讨论.


科目:初中数学 来源: 题型:
如图,直线y=kx+k(k≠0)与双曲线y=![]() 在第一象限内相交于点M,与x轴交于点A.
在第一象限内相交于点M,与x轴交于点A.

(1)求m的取值范围和点A的坐标;
(2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(海南卷)数学解析版 题型:解答题
(11·曲靖)(12分)如图:直线y=kx+3与x轴、y轴分别交于A、B两点, (1)求直线y=kx+3的解析式;
(1)求直线y=kx+3的解析式;
(2)当点C运动到什么位置时△AOC的面积是6;
(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?
若存在,请求出点C的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省扬州市江都区八年级下学期期末考试数学试卷(带解析) 题型:解答题
如图,直线y=kx+b与双曲线y= 交于点A(-1,-5)、D(5,1),并分别与x轴、y轴交于点C、B.
交于点A(-1,-5)、D(5,1),并分别与x轴、y轴交于点C、B.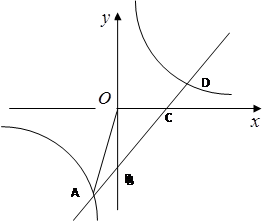
(1)求出k、b、m的值;
(2)根据图像直接写出不等式kx+b< 的解集为 ;
的解集为 ;
(3)若点E在x轴的正半轴上,是否存在以点E、C、B构成的三角形与△OAB相似?若存在,请求出E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省临淄外国语实验学校九年级中考模拟考试(2)数学试卷(解析版) 题型:选择题
如图,直线y=kx+b与坐标轴的两个交点分别为A(2,0),B(0,﹣3),
则不等式kx+b+3≥0的解为( ).
A.x≥0 B.x≤0 C.x≤2 D.x≥﹣3

查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省盐城市解放路学校中考仿真数学卷(解析版) 题型:解答题
如图,直线y=kx+k(k≠0)与双曲线y= 在第一象限内相交于点M,与x轴交于点A.
在第一象限内相交于点M,与x轴交于点A.

(1)求m的取值范围和点A的坐标;
(2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com