
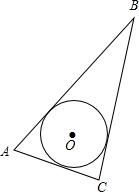
 与三角形各边都相切的圆叫做三角形的________,内切圆的________叫做三角形的内心.内心到三角形的________相等.如图,⊙O是△ABC的内切圆,△ABC是⊙O的外接三角形.
与三角形各边都相切的圆叫做三角形的________,内切圆的________叫做三角形的内心.内心到三角形的________相等.如图,⊙O是△ABC的内切圆,△ABC是⊙O的外接三角形.科目:初中数学 来源: 题型:阅读理解
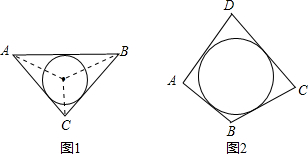 阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA
阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| l |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
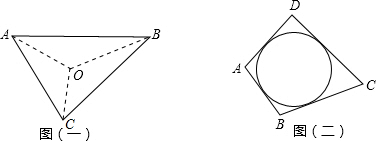
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
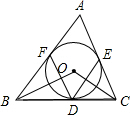 三角形的内切圆
三角形的内切圆| b+c-a |
| 2 |
| b+c-a |
| 2 |
| c+b-a |
| 2 |
| c+b-a |
| 2 |
| a+b-c |
| 2 |
| a+b-c |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2s |
| a+b+c |
| 2s |
| a+b+c |
查看答案和解析>>
科目:初中数学 来源:2011届河北省廊坊市安次区初三第一次模拟考试数学试题 题型:解答题
阅读材料:如图23—1, 的周长为
的周长为 ,面积为S,内切圆
,面积为S,内切圆 的半径为
的半径为 ,探究
,探究 与S、
与S、 之间的关系.连结
之间的关系.连结 ,
, ,
,


又 ,
, ,
,
∴
∴
解决问题 :
:
(1)利用探究的结论,计算边长分别为5,12,13的三角形内切圆半径;
(2)若四边形 存在内切圆(与各边都相切的圆),如图23—2且面积为
存在内切圆(与各边都相切的圆),如图23—2且面积为 ,各边长分别为
,各边长分别为 ,
, ,
, ,
, ,试推导四边形的内切圆半径公式;
,试推导四边形的内切圆半径公式;
(3)若一个 边形(
边形( 为不小于3的整数)存在内切圆,且面积为
为不小于3的整数)存在内切圆,且面积为 ,各边长分别为
,各边长分别为 ,
, ,
, ,
, ,
, ,合理猜想其内切圆半径公式(不需说明理由).
,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com