
【题目】如图,在平面直角坐标系中,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
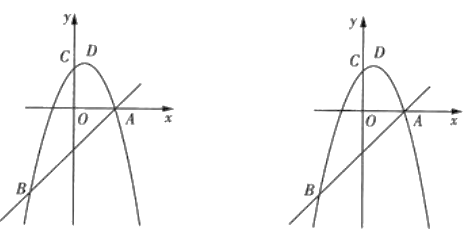
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)若向下平移抛物线,使顶点![]() 落在
落在![]() 轴上,原来的抛物线上的点
轴上,原来的抛物线上的点![]() 平移后的对应点为
平移后的对应点为![]() .若
.若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上是否存在点![]() 使
使![]() 的面积是
的面积是![]() 面积的一半?若存在,直接写出点
面积的一半?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为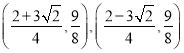 ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)把A,B两点坐标分别代入直线![]() 中求出m,n值,可得A(2,0),B(-2,-4),代入
中求出m,n值,可得A(2,0),B(-2,-4),代入![]() 求出a,b的值,可得抛物线解析式,通过配方可得顶点D的坐标;
求出a,b的值,可得抛物线解析式,通过配方可得顶点D的坐标;
(2)先求出图象向下平移的距离,再设点![]() 的坐标为
的坐标为![]() ,可得点
,可得点![]() 的坐标为
的坐标为![]() ,根据
,根据![]() ,
,![]() 轴可得点
轴可得点![]() 与点
与点![]() 关于
关于![]() 轴对称,列出方程求解即可;
轴对称,列出方程求解即可;
(3)首先求出直线y=x-2与y轴的交点E的坐标,抛物线与y轴的交点C的坐标,得O是CE的中点,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,易证
,易证![]() 要使
要使![]() 的面积是
的面积是![]() 面积的一半,则点
面积的一半,则点![]() 在过点
在过点![]() 且平行于直线
且平行于直线![]() 的直线上.因此,过点
的直线上.因此,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,联立方程组
,联立方程组![]() 求解即可;同理,在直线AB的下方也存在两点,方法同上.
求解即可;同理,在直线AB的下方也存在两点,方法同上.
![]() 将点
将点![]() 代入直线
代入直线![]() 中,
中,
得![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]()
将点![]() 代入直线
代入直线![]() ,
,
得![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
把点![]() 代入抛物线
代入抛物线![]() 中,
中,
得![]()
解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
![]() .
.
![]() 顶点
顶点![]() 的坐标为
的坐标为![]()
![]() 设点
设点![]() 的坐标为
的坐标为![]()
![]() 向下平移后点
向下平移后点![]() 落在
落在![]() 轴上.
轴上.
![]() 抛物线向下平移了
抛物线向下平移了![]() 个单位长度,
个单位长度,
则点![]() 的坐标为
的坐标为![]()
![]() ,且
,且![]() 轴.
轴.
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称
轴对称
![]() ,
,
即![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为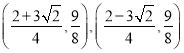
![]() 存在,设直线
存在,设直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
将![]() 代入
代入![]() 中,
中,
得![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]()
![]()
将![]() 代入
代入![]() 中,
中,
得![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
![]()
![]()
即点![]() 是线段
是线段![]() 的中点.
的中点.
过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,如解图所示.
,如解图所示.
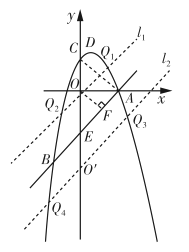
∵OC=2,OA=2,
∴CA=![]()
∵OE=2
∴AE=![]() ,CE=4
,CE=4
∵![]()
∴CA2+AE2=OE2
∴![]()
![]() 且
且![]()
![]() 要使
要使![]() 的面积是
的面积是![]() 面积的一半,
面积的一半,
则点![]() 在过点
在过点![]() 且平行于直线
且平行于直线![]() 的直线上.
的直线上.
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]() 点
点![]() 为直线
为直线![]() 与抛物线的交点.
与抛物线的交点.
过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,如解图所示,
,如解图所示,
易得直线![]() 的解析式为
的解析式为![]() .
.
联立![]()
得![]() ,
,
解得![]()
![]()
作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,
,
过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,如解图所示,
,如解图所示,
则点![]() 的坐标为
的坐标为![]() ,
,
易得直线![]() 的解析式为
的解析式为![]() .
.
同理,可知![]()
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校为了解学生每周参加家务劳动的情况,随机调查了该校部分学生每周参加家务劳动的时间.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
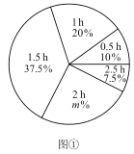

(1)本次接受调查的学生人数为___________,,图①中m的值为_________;
(2)求统计的这组每周参加家务劳动时间数据的众数、中位数和平均数;
(3)根据统计的这组每周参加家务劳动时间的样本数据,若该校共有800名学生,估计该校每周参加家务劳动的时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学:你去过黄山吗?在黄山的上山路上,有一些断断续续的台阶,如图8是其中的甲、乙段台阶路的示意图,图8中的数字表示每一级台阶的高度(单位:cm).并且数d,e,e,c,c,d的方差p,数据b,d,g,f,a,h的方差q,(10cm![]() a
a![]() b
b![]() c
c![]() d
d![]() e
e![]() f
f![]() g
g![]() h
h![]() 20cm,且 p
20cm,且 p![]() q),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
q),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
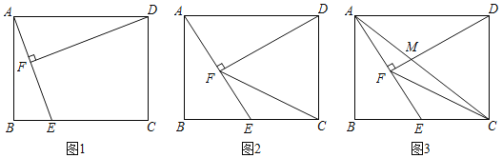
【题目】如图1,在矩形ABCD中,E是边BC上一点,连接AE,过点D作DF⊥AE于点F.
(1)若AE=DA,求证:△ABE≌△DFA.
(2)若AB=6,AD=8,且E为BC中点.
①如图2,连接CF,求sin∠DCF的值.
②如图3,连接AC交DF于点M,求CM:AM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年5月16日,“钱塘江诗路”航道全线开通,一艘游轮从杭州出发前往衢州,线路如图1所示.当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为20km/h,游轮行驶的时间记为t(h),两艘轮船距离杭州的路程s(km)关于t(h)的图象如图2所示(游轮在停靠前后的行驶速度不变).
(1)写出图2中C点横坐标的实际意义,并求出游轮在“七里扬帆”停靠的时长.
(2)若货轮比游轮早36分钟到达衢州.问:
①货轮出发后几小时追上游轮?
②游轮与货轮何时相距12km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8,BC=10,以B为圆心,任意长为半径画弧分别交BA、BC于点M和N,再分别以M、N为圆心,大于![]() MN长为半径画弧,两弧交于点P,连结BP并延长交AC于点D,若△BDC的面积为20,则△ABD的面积为( )
MN长为半径画弧,两弧交于点P,连结BP并延长交AC于点D,若△BDC的面积为20,则△ABD的面积为( )

A.20B.18C.16D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=8,BC=6,点D是射线CB上一动点,以每秒2个单位长度的速度从C出发向B运动,以CA,CD为边作矩形ACDE,直线AB与直线CE、DE的交点分别为F,G.设点D运动的时间为t(s).
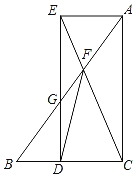
(1)BD= (用含t的代数式表示).
(2)当四边形ACDE是正方形时,求GF的长.
(3)当t为何值时,△DFG为等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com