
【题目】已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() 且经过点
且经过点![]() 动直线
动直线![]() 的解析式为
的解析式为![]()
![]() .
.
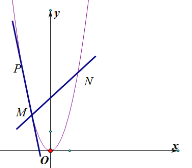
(1)求抛物线![]() 的解析式;
的解析式;
(2)将抛物线![]() 向上平移一个单位得到新的抛物线
向上平移一个单位得到新的抛物线![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点(
两点(![]() 点位于
点位于![]() 点的左边),动直线
点的左边),动直线![]() 过点
过点![]() ,与抛物线
,与抛物线![]() 的另外一个交点为点
的另外一个交点为点![]() 求证:直线
求证:直线![]() 恒过一个定点;
恒过一个定点;
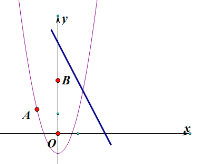
(3)已知点![]() ,且点
,且点![]() 在动直线
在动直线![]() 上,若
上,若![]() 是以
是以![]() 为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出
为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出![]() 的值.
的值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() 或
或![]() .
.
【解析】
(1)先根据顶点坐标可设其解析式的顶点式,再将点![]() 代入求解即可;
代入求解即可;
(2)先根据二次函数图象的平移得到抛物线![]() 的解析式,设点M的坐标为
的解析式,设点M的坐标为![]() ,分别求出直线MN、动直线
,分别求出直线MN、动直线![]() 的解析式,然后分别联立两个一次函数与抛物线
的解析式,然后分别联立两个一次函数与抛物线![]() 的解析式,求出点P、N的坐标,最后利用待定系数法求出直线PN的解析式,由此即可得证;
的解析式,求出点P、N的坐标,最后利用待定系数法求出直线PN的解析式,由此即可得证;
(3)设点C的坐标为![]() ,先根据两点之间的距离公式求出AB、BC的长,再根据等腰三角形的定义得出
,先根据两点之间的距离公式求出AB、BC的长,再根据等腰三角形的定义得出![]() ,从而可得一个关于
,从而可得一个关于![]() 的一元二次方程,然后利用根的判别式求解即可.
的一元二次方程,然后利用根的判别式求解即可.
(1)![]() 抛物线
抛物线![]() 的顶点坐标为
的顶点坐标为![]()
![]() 可设抛物线
可设抛物线![]() 的解析式的顶点式为
的解析式的顶点式为![]()
将点![]() 代入得:
代入得:![]() ,解得
,解得![]()
故抛物线![]() 的解析式为
的解析式为![]() ;
;
(2)由题意得:抛物线![]() 的解析式为
的解析式为![]() ,即
,即![]()
设点M的坐标为![]()
设直线MN的解析式为![]()
将点![]() ,
,![]() 代入得
代入得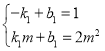 ,解得
,解得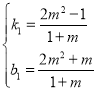
则直线MN的解析式为![]()
联立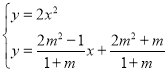
设点![]()
则![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的两根
的两根
由根与系数的关系得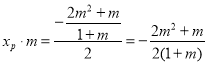
解得![]()
将![]() 代入抛物线
代入抛物线![]() 的解析式得:
的解析式得: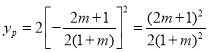
即![]()
将点![]() 代入
代入![]() 得
得![]() ,解得
,解得![]()
则动直线![]() 的解析式为
的解析式为![]()
联立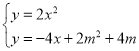
设点![]()
则![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的两根
的两根
由根与系数的关系得![]()
解得![]()
将![]() 代入抛物线
代入抛物线![]() 的解析式得:
的解析式得:![]()
即![]()
设直线PN的解析式为![]()
将![]() 代入得:
代入得:![]()
将![]() 代入得:
代入得:![]()
解得
则直线PN的解析式为![]()
由此可知,当![]() 时,
时,![]()
即无论m取何值,直线PN恒过定点![]() ;
;
(3)设点C的坐标为![]()
![]()
![]() ,
,![]()
若![]() 是以
是以![]() 为顶角的等腰三角形,则
为顶角的等腰三角形,则![]() ,从而有
,从而有![]()
即![]()
整理得![]()
因为这样的等腰三角形有且只存在一个
所以关于![]() 的一元二次方程
的一元二次方程![]() 有两个相等的实数根
有两个相等的实数根
则此方程的根的判别式![]()
解得![]() 或
或![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,斜坡AB的长为65米,坡度i=1∶2.4,BC⊥AC.
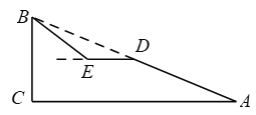
(参考三角函数:sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
(1)求斜坡的高度BC.
(2)现计划在斜坡AB的中点D处挖去部分坡体,修建一个平行于水平线CA的平台DE和一条新的斜坡BE,若斜坡BE的坡角为37°,求平台DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:6cos45°+(![]() ﹣1.73)0+|5﹣3
﹣1.73)0+|5﹣3![]() |+42017×(﹣0.25)2017;
|+42017×(﹣0.25)2017;
(2)先化简,再求值:(![]() ﹣a+1)÷
﹣a+1)÷![]() ﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“长跑”是中考体育考试项目之一.某中学为了解九年级学生“长跑”的情况,随机抽取部分九年级学生,测试其长跑成绩(男子1000米,女子800米),按长跑的时间的长短依次分为A,B,C,D四个等级进行统计,并绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
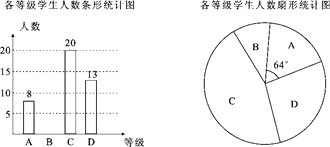
(1)在这次调查中共抽取了 名学生,扇形统计图中,D类所对应的扇形圆心角大小为 ;
(2)所抽取学生“长跑”测试成绩的中位数会落在 等级;
(3)若该校九年级共有900名学生,请你估计该校C等级的学生约在多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,将
边上,将![]() 沿着
沿着![]() 折叠后得到
折叠后得到![]() ,连接
,连接![]() 并使得
并使得![]() 最小,请画出符合题意的点
最小,请画出符合题意的点![]() ;
;
问题探究:
(2)如图②,已知在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,求
,求![]() 的最大值;
的最大值;
问题解决:
(3)西安大明宫遗址公园是世界文化遗产,全国重点文物保护单位,为了丰富同学们的课外学习生活,培养同学们的探究实践能力,周末光明中学的张老师在家委会的协助下,带领全班同学去大明宫开展研学活动.在公园开设的一处沙地考古模拟场地上,同学们参加了一次模拟考古游戏.张老师为同学们现场设计了一个四边形![]() 的活动区域,如图③所示,其中
的活动区域,如图③所示,其中![]() 为一条工作人员通道,同学们的入口设在点
为一条工作人员通道,同学们的入口设在点![]() 处,
处,![]() ,
,![]() ,
,![]() ,
,![]() 米.在上述条件下,小明想把宝物藏在距入口
米.在上述条件下,小明想把宝物藏在距入口![]() 尽可能远的
尽可能远的![]() 处让小鹏去找,请问小明的想法是否可以实现?如果可以,请求出
处让小鹏去找,请问小明的想法是否可以实现?如果可以,请求出![]() 的最大值及此时
的最大值及此时![]() 区域的面积,如果不能,请说明理由.
区域的面积,如果不能,请说明理由.
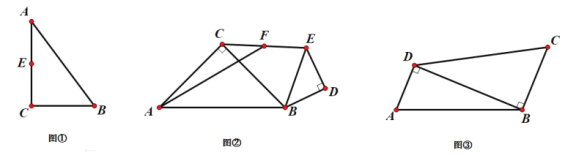
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的两条邻边长分别为6和8,则第n个菱形的周长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,AB=AC,∠A=40O,延长AC到D,使CD=BC,点P是ΔABD的内心,则∠BPC=

A. 105° B. 110° C. 130° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为争创文明城市,我市交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,并将两次收集的数据制成如下统计图表.

类别 | 人数 | 百分比 |
A | 68 | 6.8% |
B | 245 | b% |
C | a | 51% |
D | 177 | 17.7% |
总计 | c | 100% |
根据以上提供的信息解决下列问题:
(1)a= ,b= c=
(2)若我市约有30万人使用电瓶车,请分别计算活动前和活动后全市骑电瓶车“都不戴”安全帽的人数.
(3)经过某十字路口,汽车无法继续直行只可左转或右转,电动车不受限制,现有一辆汽车和一辆电动车同时到达该路口,用画树状图或列表的方法求汽车和电动车都向左转的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com