
【题目】如图,在平面直角坐标系中的三点A(1,0),B(-1,0),P(0,-1),将线段AB沿y轴向上平移m(m>0)个单位长度,得到线段CD,二次函数y=a(x-h)2+k的图象经过点P,C,D.
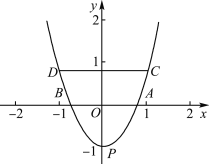
(1)当m=1时,a=______;当m=2时,a=______;
(2)猜想a与m的关系,并证明你的猜想;
(3)将线段AB沿y轴向上平移n(n>0)个单位长度,得到线段C1D1,点C1,D1分别与点A,B对应,二次函数y=2a(x-h)2+k的图象经过点P,C1,D1.
①求n与m之间的关系;
②当△COD1是直角三角形时,直接写出a的值.
【答案】(1)2,3;(2)a=m+1.证明见解析;(3)①![]() ;②当△COD1是直角三角形时,a的值是
;②当△COD1是直角三角形时,a的值是![]() 或2.
或2.
【解析】
(1)分别把![]() 和
和![]() 代入可得
代入可得![]() 的坐标,根据抛物线顶点
的坐标,根据抛物线顶点![]() 写出解析式为:
写出解析式为:![]() ,再代入
,再代入![]() 或
或![]() 的坐标即可;
的坐标即可;
(2)根据线段![]() 沿
沿![]() 轴向上平移
轴向上平移![]() 个单位长度,得到线段
个单位长度,得到线段![]() ,写出
,写出![]() 和
和![]() 的坐标,同理将
的坐标,同理将![]() 的坐标代入解析式中可得结论;
的坐标代入解析式中可得结论;
(3)①同理可得:![]() ,由(2)中得:
,由(2)中得:![]() ,列等式可得;
,列等式可得;
②分别以三个顶点为直角顶点,由勾股定理列方程可得![]() 的值.
的值.
解:(1)当![]() 时,
时,![]() ,
,![]() ,
,
![]() 抛物线顶点
抛物线顶点![]() ,
,
![]() ,
,
把![]() 代入得:
代入得:![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
![]() 抛物线顶点
抛物线顶点![]() ,
,
![]() ,
,
把![]() 代入得:
代入得:![]() ,
,
![]() ,
,
故答案为:2;3;
(2)![]() ,理由是:
,理由是:
由题意得:![]() ,
,![]()
把![]() 代入抛物线的解析式
代入抛物线的解析式![]() 中得:
中得:![]() ,
,
![]()
(3)①由题意得:![]() ,
,![]() ,
,
把![]() 代入抛物线的解析式
代入抛物线的解析式![]() 中得:
中得:![]() ,
,
![]() ,
,
由(2)知:![]() ,
,
![]() ,
,
![]() ;
;
②分三种情况:
![]() ,
,![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() 是直角三角形,如图1,
是直角三角形,如图1,
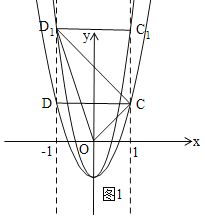
由勾股定理得:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (舍
(舍![]() ,
,![]() ;
;
![]() 当
当![]() 时,
时,![]() 是直角三角形,如图2,
是直角三角形,如图2,
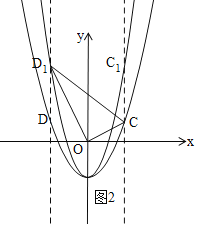
由勾股定理得:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (舍
(舍![]() ,
,![]() ;
;
![]() 当
当![]() ,
,![]() 是直角三角形,
是直角三角形,
同理得:![]() ,
,
![]() ,
,
![]() ,
,
△![]() ,
,
此方程无实数解,
综上所述,当![]() 是直角三角形时,
是直角三角形时,![]() 的值是
的值是![]() 或2.
或2.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②当x>1时,y随x的增大而减少;③m>-1;④当a=-1时,b=3;其中,判断正确的序号是( )
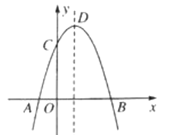
A.①②B.②③C.①③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线l及直线l外一点P.
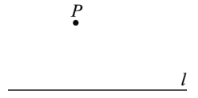
求作:直线![]() ,使得
,使得![]() .
.
作法:如图,

①任意取一点K,使点K和点P在直线l的两旁;
②以P为圆心,![]() 长为半径画弧,交l于点
长为半径画弧,交l于点![]() ,连接
,连接![]() ;
;
③分别以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,两弧相交于点Q(点Q和点A在直线
长为半径画弧,两弧相交于点Q(点Q和点A在直线![]() 的两旁);
的两旁);
④作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接![]() ,
,
![]() ______,
______,![]() ______,
______,
![]() 四边形
四边形![]() 是平行四边形(__________)(填推理依据).
是平行四边形(__________)(填推理依据).
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为
的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为![]() ,AD=2,则△ACO的面积为_________.
,AD=2,则△ACO的面积为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.如图2,则抛物线y=x![]() 的“完美三角形”斜边AB的长________.
的“完美三角形”斜边AB的长________.
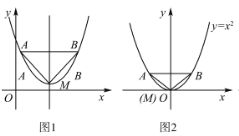
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是抛物线的顶点.
是抛物线的顶点.
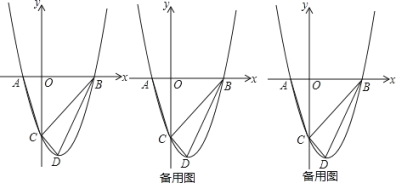
(1)求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
(2)连接![]() ,
,![]() ,
,![]() ,若点
,若点![]() 为抛物线上一动点,设点
为抛物线上一动点,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,求
时,求![]() 的值(点
的值(点![]() 不与点
不与点![]() 重合);
重合);
(3)连接![]() ,将
,将![]() 沿
沿![]() 轴正方向平移,设移动距离为
轴正方向平移,设移动距离为![]() ,当点
,当点![]() 和点
和点![]() 重合时,停止运动,设运动过程中
重合时,停止运动,设运动过程中![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的函数关系式,并写出相应自变量
之间的函数关系式,并写出相应自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】延迟开学期间,学校为了全面分析学生的网课学习情况,进行了一次抽样调查(把学习情况分为三个层次,![]() :能主动完成老师布置的作业并合理安排课外时间自主学习;
:能主动完成老师布置的作业并合理安排课外时间自主学习;![]() :只完成老师布置的作业;
:只完成老师布置的作业;![]() :不能完成老师布置的作业),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:
:不能完成老师布置的作业),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:


(1)此次抽样调查中,共调查了__________名学生;
(2)将条形图补充完整;
(3)图2中![]() 所占的圆心角的度数为__________度;
所占的圆心角的度数为__________度;
(4)如果学校开学后对![]() 层次的学生进行奖励,根据抽样调查结果,请你估计该校1600名学生中大约有多少名学生能获得奖励?
层次的学生进行奖励,根据抽样调查结果,请你估计该校1600名学生中大约有多少名学生能获得奖励?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息.
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价.
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A、B两类图书共1000本 2.A类图书不少于600本 | |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划投资![]() 、
、![]() 两种产品,若只投资
两种产品,若只投资![]() 产品,所获得利润
产品,所获得利润![]() (万元)与投资金额
(万元)与投资金额![]() (万元)之间的关系如图所示,若只投资
(万元)之间的关系如图所示,若只投资![]() 产品,所获得利润
产品,所获得利润![]() (万元)与投资金额
(万元)与投资金额![]() (万元)的函数关系式为
(万元)的函数关系式为![]() .
.
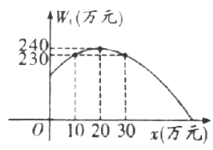
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若投资![]() 产品所获得利润的最大值比投资
产品所获得利润的最大值比投资![]() 产品所获得利润的最大值少
产品所获得利润的最大值少![]() 万元,求
万元,求![]() 的值;
的值;
(3)该公司筹集![]() 万元资金,同时投资
万元资金,同时投资![]() 、
、![]() 两种产品,设投资
两种产品,设投资![]() 产品的资金为
产品的资金为![]() 万元,所获得的总利润记作
万元,所获得的总利润记作![]() 万元,若
万元,若![]() 时,
时,![]() 随
随![]() 的增大而减少,求
的增大而减少,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com