
【题目】四个形状大小相同的等腰三角形按如图所示方式摆放,已知![]() ,
,![]() ,若点
,若点![]() 落在
落在![]() 的延长线上,则图中阴影部分的面积为( )
的延长线上,则图中阴影部分的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
利用已知条件判定菱形,然后由四边形OHGK是平行四边形得OK=2,再由相似三角形,利用相似比求得OB,即可得其面积.
连接EF、GF,将△OHC沿点O顺时针旋转180°,如图所示:

由题意,得OB=OC=OA,∠EAO=∠AOF=∠FAO=∠AOE,GH⊥BO
∴AE∥FO,AF∥EO,GH∥OA
∴四边形AEOF为平行四边形
∴AE=EO
∴四边形AEOF为菱形
∴OH∥BF
∴四边形OHGK为平行四边形
∴OK=2
∵![]()
∴△ABC为等腰三角形
∴∠GOF=90°,OG=OF
设四个相同的等腰三角形的腰长为![]()
∵∠KOF=∠OBF,∠OFB=∠KFO
∴△OFB∽△KFO
∴![]() 即
即
∴![]()
∴阴影部分的面积为![]()
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如果抛物线y=ax2+bx+c过定点M(1,0),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的解析式.小敏写出了一个正确的答案:y=2x2+3x-5.请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c,求该抛物线的顶点最低时的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且当
,且当![]() 和
和![]() 时二次函数的函数值
时二次函数的函数值![]() 相等.
相等.
(![]() )求实数
)求实数![]() 、
、![]() 的值.
的值.
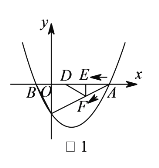
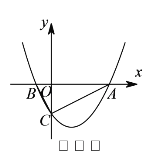
(![]() )如图
)如图![]() ,动点
,动点![]() 、
、![]() 同时从
同时从![]() 点出发,其中点
点出发,其中点![]() 以每秒
以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 边向终点
边向终点![]() 运动,点
运动,点![]() 以每秒
以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向运动,当点
方向运动,当点![]() 停止运动时,点
停止运动时,点![]() 随之停止运动.设运动时间为
随之停止运动.设运动时间为![]() 秒.连接
秒.连接![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在点
落在点![]() 处,得到
处,得到![]() .
.
①是否存在某一时刻![]() ,使得
,使得![]() 为直角三角形?若存在,求出
为直角三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
②设![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例y=![]() 的图象与一次函数y=kx﹣3的图象在第一象限内交于A(4,a).
的图象与一次函数y=kx﹣3的图象在第一象限内交于A(4,a).
(1)求一次函数的解析式;
(2)若直线x=n(0<n<4)与反比例函数和一次函数的图象分别交于点B,C,连接AB,若△ABC是等腰直角三角形,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
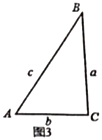
【题目】小迪同学在学勾股定理时发现一类特殊三角形:在一个三角形中,如果一个角是另一个角的2倍,那么称这个三角形为“倍角三角形”.
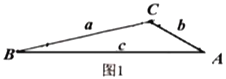
如图1,在倍角![]() 中,
中,![]() ,
,![]() 、
、![]() 、
、![]() 的对边分别记为
的对边分别记为![]() ,
,![]() ,
,![]() ,三角形的三边
,三角形的三边![]() ,
,![]() ,
,![]() 有什么关系呢?让我们一起来探索……
有什么关系呢?让我们一起来探索……
(1)已知“倍角三角形”的一个内角为![]() ,则这个三角形的另两个角的度数分别为______
,则这个三角形的另两个角的度数分别为______
(2)小迪同学先从特殊的“倍角三角形”入手研究,请你结合图2和图3填写下表:
三角形 | 角的已知量 |
|
|
图2 |
| ______ | ______ |
图3 |
| ______ |
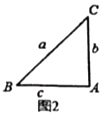
小迪同学根据上表,提出一般性猜想:在“倍角三角形”中,![]() ,那么
,那么![]() ,
,![]() ,
,![]() 三边满足:______;
三边满足:______;
(3)如图1:在倍角三角形中,![]() ,
,![]() 、
、![]() 、
、![]() 的对边分别记为
的对边分别记为![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,已知
,已知![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)如图,观察并猜想![]() 和
和![]() 有怎样的数量关系?并说明理由.
有怎样的数量关系?并说明理由.
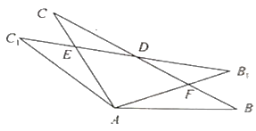
(2)筝形的定义:两组邻边分别相等的四边形叫做筝形. 如上图,证明四边形![]() 是筝形.
是筝形.
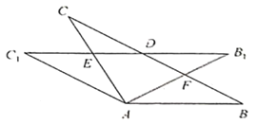
(3)如图,若![]() ,其他条件不变,求
,其他条件不变,求![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com