
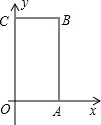
 如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).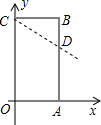 解:(1)B点坐标为(3,5).
解:(1)B点坐标为(3,5).| CB+BD |
| CO+OA+AB-BD |
| 1 |
| 3 |
| 3+BD |
| 13-BD |
| 1 |
| 3 |
|
|
| 1 |
| 3 |


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
 如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).查看答案和解析>>
科目:初中数学 来源:2011年广东省揭阳立才中考模拟数学卷 题型:解答题
如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足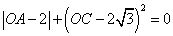 .
.
⑴求B、C两点的坐标.
⑵把△ABC沿AC对折,点B落在点B′处,线段AB′与x轴交于点D,求直线BB′的解析式.
⑶在直线BB′上是否存在点P,使△ADP为直角三角形?若存在,请直接写出
P 点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
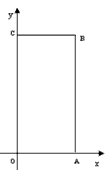
如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5)。
(1)直接写出B点坐标;
(2)若过点C的直线CD交AB边于点D,且把矩形OABC的周长分为1∶3两部分,求直线CD的解析式;
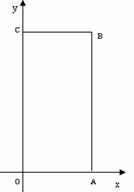
查看答案和解析>>
科目:初中数学 来源:贵州省期末题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com