
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的动点(不与点
上的动点(不与点![]() ,
,![]() 重合),
重合),![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() .则对于下列结论:①
.则对于下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中错误结论的个数是( )
,其中错误结论的个数是( )
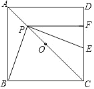
A.0B.1C.2D.3
【答案】B
【解析】
连接PD,证明△PBC≌△PDC得出∠PBC=∠PDE,PB=PD,证出∠PDE=∠PED,得出PD=PE,因此PE=PB,①正确;由等腰三角形的性质得出DF=EF,②正确;
作PH⊥AD于点H,则![]() 得出
得出![]() ,即
,即![]() ,得出
,得出![]() ,③正确;证出PF∥AD,得出
,③正确;证出PF∥AD,得出![]() ,由DF≠CE得出
,由DF≠CE得出![]() ,④错误;即可得出结论.
,④错误;即可得出结论.
连接PD,如图1所示: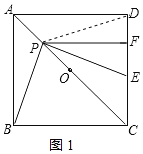
∵四边形ABCD是正方形,
∴BC=DC,∠BCP=∠DCP,
在△PBC和△PDC中,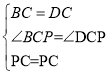 ,
,
∴△PBC≌△PDC(SAS)
∴∠PBC=∠PDE,PB=PD,
∵PB⊥PE,∠BCD=90°,
∴∠PBC+∠PEC=360°-∠BPE-∠BCE=180°
∵∠PEC+∠PED=180°,
∴∠PBC=∠PED,
∴∠PDE=∠PED,
∴PD=PE,
∴PE=PB,①正确;
∵PD=PE,PF⊥CD,
∴DF=EF,②正确;
作PH⊥AD于点H,如图2所示: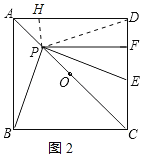
则![]()
∴![]() ,即
,即![]() ,
,
∴![]() ,③正确;
,③正确;
∵PF⊥CD,AD⊥CD,
∴PF∥AD,
∴![]() ,
,
∵DF≠CE,
∴![]() ,④错误;
,④错误;
错误结论的个数有1个;
故答案为:B.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本价为50元/千克,规定每千克售价不低于成本价,且不高于85元.经过市场调查,该商品每天的销售量![]() (千克)与售价
(千克)与售价![]() (元/千克)满足一次函数关系,部分数据如下表:
(元/千克)满足一次函数关系,部分数据如下表:
售价 | 50 | 60 | 70 |
销售量 | 120 | 100 | 80 |
(1)求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
(2)设该商品每天的总利润为![]() (元),则当售价
(元),则当售价![]() 定为多少元/千克时,超市每天能获得最大利润?最大利润是多少元?
定为多少元/千克时,超市每天能获得最大利润?最大利润是多少元?
(3)如果超市要获得每天不低于1600元的利润,且符合超市自己的规定,那么该商品的售价![]() 的取值范围是多少?请说明理由.
的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
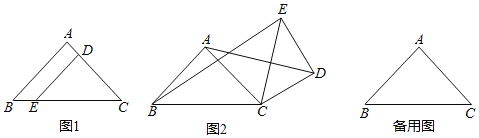
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D,E两点分别在AC,BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现:当α=0°时,![]() 的值为 ;
的值为 ;
(2)拓展探究:当0°≤α<360°时,若△EDC旋转到如图2的情况时,求出![]() 的值;
的值;
(3)问题解决:当△EDC旋转至A,B,E三点共线时,若设CE=5,AC=4,直接写出线段BE的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于线段![]() 和点
和点![]() ,当
,当![]() ,且
,且![]() 时,称点
时,称点![]() 为线段
为线段![]() 的“等距点”.特别地,当
的“等距点”.特别地,当![]() ,且
,且![]() 时,称点
时,称点![]() 为线段
为线段![]() 的“强等距点”.在平面直角坐标系
的“强等距点”.在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() .
.
(1)有4个点:![]() ,
,![]() ,
,![]() ,
,![]() .线段
.线段![]() 的“等距点”是 ;其中线段
的“等距点”是 ;其中线段![]() 的“强等距点”是 .
的“强等距点”是 .
(2)设第四象限有一点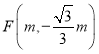 ,点
,点![]() 是线段
是线段![]() 的“强等距点”.
的“强等距点”.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②当点![]() 又为线段
又为线段![]() 的“等距点”时,求
的“等距点”时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为
S3;则S3﹣S2= .
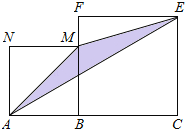
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,
边上,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
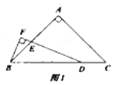
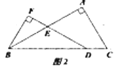
(1)如图1,当![]() 时:①
时:①![]() 的度数为__________;②求证;
的度数为__________;②求证;![]() ;
;
(2)如图2,当![]() 时,求
时,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,对于直线![]() 同侧的
同侧的![]() 、
、![]() 两点,若在
两点,若在![]() 上的点
上的点![]() 满足
满足![]() ,则称
,则称![]() 为
为![]() 、
、![]() 两点在
两点在![]() 上的反射点,
上的反射点,![]() 与
与![]() 的和称为
的和称为![]() 、
、![]() 两点的反射距离.
两点的反射距离.

(1)如图2,在边长为2的正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 、
、![]() 两点在直线
两点在直线![]() 上的反射点,求
上的反射点,求![]() 、
、![]() 两点的反射距离;
两点的反射距离;
(2)如图3,![]() 内接于
内接于![]() ,直径
,直径![]() 为4,
为4,![]() ,点
,点![]() 为劣弧
为劣弧![]() 上一动点,点
上一动点,点![]() 为
为![]() 、
、![]() 两点在
两点在![]() 上的反射点,当
上的反射点,当![]() 、
、![]() 两点的反射距离最大时,求劣弧
两点的反射距离最大时,求劣弧![]() 的长;
的长;
(3)如图4,在平面直角坐标系中,抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,顶点为
,顶点为![]() ,若点
,若点![]() 为点
为点![]() 、
、![]() 在
在![]() 上的反射点,同时点
上的反射点,同时点![]() 为点
为点![]() 、
、![]() 在
在![]() 上的反射点.
上的反射点.
①请判断线段![]() 和
和![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
②求![]() 、
、![]() 两点的反射距离与
两点的反射距离与![]() 、
、![]() 两点的反射距离的比值.
两点的反射距离的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=3,点P是边AB上的一动点,连接DP,
(1)若将△DAP沿DP折叠,点A落在矩形的对角线上点A处,试求AP的长;
(2)点P运动到某一时刻,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP与PE折叠,点A与点B分别落在点A,B处,若P,A,B三点恰好在同一直线上,且AB=2,试求此时AP的长.
(3)当点P运动到边AB的中点处时,过点P作直线PG交BC于点G,将△DAP与△PBG分别沿DP与PG折叠,点A与点B重合于点F处,请直接写出F到BC的距离.
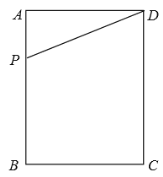
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com