
【题目】如图,在平面直角坐标系中,正方形![]() 的顶点A的坐标为
的顶点A的坐标为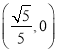 ,顶点D的坐标为
,顶点D的坐标为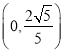 ,延长
,延长![]() 交
交![]() 轴于点A,作正方形
轴于点A,作正方形![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ,按这样的规律进行下去,第2021个正方形的周长为( )
,按这样的规律进行下去,第2021个正方形的周长为( )
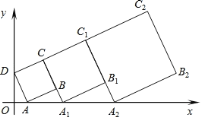
A.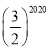 B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
推出AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA,求出∠ADO=∠BAA1,证△DOA∽△ABA1,得出![]() =
=![]() =
=![]() ,求出AB,BA1,求出边长A1C=
,求出AB,BA1,求出边长A1C=![]() ,求出周长即可;求出第2个正方形的边长是(
,求出周长即可;求出第2个正方形的边长是(![]() )2,求出周长,再求出第3个正方形的周长;依此类推得出第2021个正方形的边长,求出周长即可.
)2,求出周长,再求出第3个正方形的周长;依此类推得出第2021个正方形的边长,求出周长即可.
解:∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA,
∴∠ADO+∠DAO=90°,∠DAO+∠BAA1=90°,
∴∠ADO=∠BAA1,
∵∠DOA=∠ABA1,
∴△DOA∽△ABA1,
∴![]() =
=![]() =
=![]() ,
,
∵AB=AD=![]() =1,
=1,
∴BA1=![]() ,
,
∴第2个正方形A1B1C1C的边长A1C=A1B+BC=![]() +1=
+1=![]() ,周长是4×
,周长是4×![]() ,
,
同理第3个正方形的边长是![]() ,周长是4×(
,周长是4×(![]() )2;
)2;
第4个正方形的边长是(![]() )3,周长是4×(
)3,周长是4×(![]() )3;
)3;
…,
第2021个正方形的边长是(![]() )2020,周长是4×(
)2020,周长是4×(![]() )2020,
)2020,
故选:C.


科目:初中数学 来源: 题型:
【题目】新学期复学后,学校为了保障学生的出行安全,随机调查了部分学生的上学方式(每位学生从乘私家车、坐公交、骑车和步行4种方式中限选1项),根据调查数据制作了如图所示的不完整的统计表和扇形统计图.

(1)本次学校共调查了 名学生,![]() ,
,![]() ;
;
(2)求扇形统计图中“步行”对应扇形的圆心角;
(3)甲、乙两位同学住在同一小区,且都坐公交车上学,有![]() 、
、![]() 、
、![]() 三路公交车途径该小区和学校,假设甲、乙两位同学坐这三路公交车是等可能的,请用列表或画树状图的方法求某日甲、乙两位同学坐同一路公交车到学校的概率.
三路公交车途径该小区和学校,假设甲、乙两位同学坐这三路公交车是等可能的,请用列表或画树状图的方法求某日甲、乙两位同学坐同一路公交车到学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,正方形![]() 与正方形
与正方形![]() 有公共的顶点
有公共的顶点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
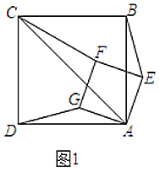
①求证:![]() ;
;
②求![]() 的值;
的值;
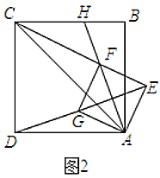
(2)将图1中的正方形![]() 旋转到图2的位置,当
旋转到图2的位置,当![]() ,
,![]() ,
,![]() 在一条直线上,若
在一条直线上,若![]() ,求正方形
,求正方形![]() 的边长.
的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
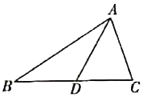
(1)如图,![]() 是
是![]() 的中线,则
的中线,则![]() __________
__________![]() ;(填“
;(填“![]() ”“
”“![]() ”或“
”或“![]() ”)
”)
问题探究
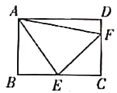
(2)如图,在矩形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上任意一点,当
上任意一点,当![]() 的周长最小时,求
的周长最小时,求![]() 的长;
的长;
问题解决
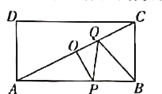
(3)如图,在矩形![]() 中,
中,![]() ,点
,点![]() 为对角线
为对角线![]() 的中点,点
的中点,点![]() 为
为![]() 上任意一点,点
上任意一点,点![]() 为
为![]() 上任意一点,连接
上任意一点,连接![]() ,是否存在这样的点
,是否存在这样的点![]() ,使折线
,使折线![]() 的长度最小?若存在,请确定点
的长度最小?若存在,请确定点![]() 的位置,并求出折线
的位置,并求出折线![]() 的最小长度;若不存在,请说明理由.
的最小长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区计划对1200m2的区域进行绿化,经投标由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且甲、乙两队在分别独立完成面积为300m2区域的绿化时,甲队比乙队少用3天.
⑴ 甲、乙两施工队每天分别能完成绿化的面积是多少?
⑵ 设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
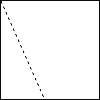
A.直角三角形B.平行四边形C.菱形D.等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,0<x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
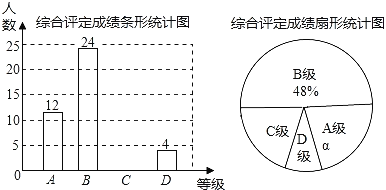
(1)在这次调查中,一共抽取了 名学生;
(2)扇形统计图中,α= %,C级对应的圆心角为 度;
(3)请你利用你所学的统计知识,估计本次抽取所有学生的综合评定成绩的平均分.
查看答案和解析>>
科目:初中数学 来源: 题型:
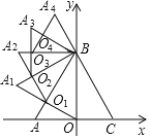
【题目】如图,边长为4的等边△ABC,AC边在x轴上,点B在y轴的正半轴上,以OB为边作等边△OBA1,边OA1与AB交于点O1,以O1B为边作等边△O1BA2,边O1A2与A1B交于点O2,以O2B为边作等边△O2BA3,边O2A3与A2B交于点O3,…,依此规律继续作等边△On﹣1BAn,则![]() 的横坐标_____.
的横坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com