
【题目】已知![]() 在数轴上的位置如图所示,所对应的点分别为
在数轴上的位置如图所示,所对应的点分别为![]() .
.
![]()
(1)在数轴上表示![]() 的点与表示
的点与表示![]() 的点之间的距离为 ;由此可得点
的点之间的距离为 ;由此可得点![]() 之间的距离为
之间的距离为
(2)化简:![]()
(3)若![]() 的倒数是它本身,
的倒数是它本身,![]() 的绝对值的相反数是
的绝对值的相反数是![]() ,
,![]() 是数轴上表示
是数轴上表示![]() 的一点,且
的一点,且![]() ,求
,求![]() 所表示的数.
所表示的数.
【答案】(1)4;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 所表示的数为
所表示的数为![]() 或
或![]() .
.
【解析】
(1)根据数轴的定义:两点之间的距离即可得;
(2)根据数轴的定义,得出![]() 的符号、绝对值大小,再根据绝对值运算化简即可;
的符号、绝对值大小,再根据绝对值运算化简即可;
(3)先根据平方数、倒数、相反数的定义求出![]() 的值,再根据绝对值运算化简求值即可得.
的值,再根据绝对值运算化简求值即可得.
(1)由数轴的定义得:在数轴上表示![]() 的点与表示
的点与表示![]() 的点之间的距离为
的点之间的距离为![]() ;点
;点![]() 之间的距离为
之间的距离为![]()
故答案为:4;![]() ;
;
(2)由![]() 在数轴上的位置可知:
在数轴上的位置可知:![]()
则![]()
![]()
![]() ;
;
(3)由![]() 在数轴上的位置可知:
在数轴上的位置可知:![]()
由![]() 得,
得,![]() 或
或![]() (舍去)
(舍去)
由![]() 的倒数是它本身得,
的倒数是它本身得,![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
由![]() 的绝对值的相反数是
的绝对值的相反数是![]() 得,
得,![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
将![]() 代入得
代入得![]()
根据数轴的定义、绝对值运算分以下四部分讨论:
①当![]() 时,
时,![]()
解得![]() ,符合题设
,符合题设
②当![]() 时,
时,![]()
解得![]() ,不符题设,舍去
,不符题设,舍去
③当![]() 时,
时,![]()
解得![]() ,不符题设,舍去
,不符题设,舍去
④当![]() 时,
时,![]()
解得![]() ,符合题设
,符合题设
综上,![]() 所表示的数为
所表示的数为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,将△ABD沿AB向下平移使A点到达B点,得到△BEC,下列说法正确的是( )
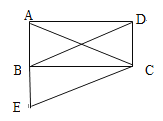
A. △ACE一定是等腰三角形B. △ACE一定是等边三角形
C. △ACE一定是锐角三角形D. △ACE不可能是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书报亭开设两种租书方式:一种是零星租书,每册收费1元;另一种是会员卡租书,办卡费每月12元,租书费每册0.4元.小军经常来该店租书,若每月租书数量为x册.
(1)写出零星租书方式应付金额![]() (元)与租书数量x(册)之间的函数关系式。
(元)与租书数量x(册)之间的函数关系式。
(2)写出会员卡租书方式应付金额![]() (元)与租书数量x(册)之间的函数关系式.
(元)与租书数量x(册)之间的函数关系式.
(3)小军选取哪种租书方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
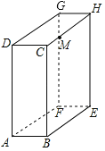
【题目】如图,长方体的长BE=20cm,宽AB=10cm,高AD=15cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE⊥AB,BD⊥AC,垂足分别为E、D,BD、CE交于点O,AB=AC,∠B=20°,则∠AOD=( )

A. 20°B. 40°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A,B两点对应的数分别为a,b,且a,b满足|a+20|=﹣(b﹣13)2,点C对应的数为16,点D对应的数为﹣13.
(1)求a,b的值;
(2)点A,B沿数轴同时出发相向匀速运动,点A的速度为6个单位/秒,点B的速度为2个单位/秒,若t秒时点A到原点的距离和点B到原点的距离相等,求t的值;
(3)在(2)的条件下,点A,B从起始位置同时出发.当A点运动到点C时,迅速以原来的速度返回,到达出发点后,又折返向点C运动.B点运动至D点后停止运动,当B停止运动时点A也停止运动.求在此过程中,A,B两点同时到达的点在数轴上对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,
<3,
∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2)
﹣2)
请解答:
(1)![]() 整数部分是 ,小数部分是 .
整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求|a﹣b|+
的整数部分为b,求|a﹣b|+![]() 的值.
的值.
(3)已知:9+![]() =x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
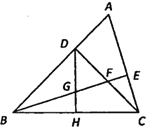
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com