
【题目】(本题满分10分)
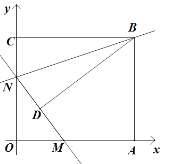
如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x-15|+=0(OB>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,连接BN.将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=.
⑴ 求点B的坐标.
⑵ 求直线BN的解析式.
⑶ 将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB的面积S关于运动的时间t(0<t≤13)的函数关系式.
【答案】(1)B(15,13);(2)直线BN的解析式为y=![]() x+8;(3)S=
x+8;(3)S=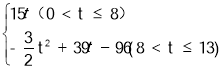 .
.
【解析】
试题分析:(1)由非负数的性质可求得x、y的值,则可求得B点坐标;
(2)过D作EF⊥OA于点E,交CB于点F,由条件可求得D点坐标,且可求得![]() ,结合DE∥ON,利用平行线分线段成比例可求得OM和ON的长,则可求得N点坐标,利用待定系数法可求得直线BN的解析式;
,结合DE∥ON,利用平行线分线段成比例可求得OM和ON的长,则可求得N点坐标,利用待定系数法可求得直线BN的解析式;
(3)设直线BN平移后交y轴于点N′,交AB于点B′,当点N′在x轴上方时,可知S即为BNN′B′的面积,当N′在y轴的负半轴上时,可用t表示出直线B′N′的解析式,设交x轴于点G,可用t表示出G点坐标,由S=S四边形BNN′B′﹣S△OGN′,可分别得到S与t的函数关系式.
试题解析:(1)∵|x﹣15|+![]() =0,
=0,
∴x=15,y=13,
∴OA=BC=15,AB=OC=13,
∴B(15,13);
(2)如图1,过D作EF⊥OA于点E,交CB于点F,
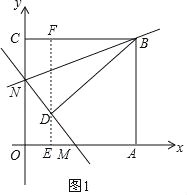
由折叠的性质可知BD=BC=15,∠BDN=∠BCN=90°,
∵tan∠CBD=![]() ,
,
∴![]() ,且BF2+DF2=BD2=152,解得BF=12,DF=9,
,且BF2+DF2=BD2=152,解得BF=12,DF=9,
∴CF=OE=15﹣12=3,DE=EF﹣DF=13﹣9=4,
∵∠CND+∠CBD=360°﹣90°﹣90°=180°,且∠ONM+∠CND=180°,
∴∠ONM=∠CBD,
∴![]() ,
,
∵DE∥ON,
∴![]() ,且OE=3,
,且OE=3,
∴![]() ,解得OM=6,
,解得OM=6,
∴ON=8,即N(0,8),
把N、B的坐标代入y=kx+b可得
![]() ,解得
,解得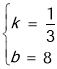 ,
,
∴直线BN的解析式为y=![]() x+8;
x+8;
(3)设直线BN平移后交y轴于点N′,交AB于点B′,
当点N′在x轴上方,即0<t≤8时,如图2,
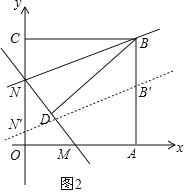
由题意可知四边形BNN′B′为平行四边形,且NN′=t,
∴S=NN′OA=15t;
当点N′在y轴负半轴上,即8<t≤13时,设直线B′N′交x轴于点G,如图3,
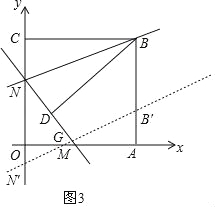
∵NN′=t,
∴可设直线B′N′解析式为y=![]() x+8﹣t,
x+8﹣t,
令y=0,可得x=3t﹣24,
∴OG=24,
∵ON=8,NN′=t,
∴ON′=t﹣8,
∴S=S四边形BNN′B′﹣S△OGN′=15t﹣![]() (t﹣8)(3t﹣24)=﹣
(t﹣8)(3t﹣24)=﹣![]() t2+39t﹣96;
t2+39t﹣96;
综上可知S与t的函数关系式为S=.


科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1 , 再以正方形的对角线OA2作正方形OA1A2B1 , …,依此规律,则点A8的坐标是( )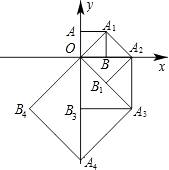
A.(﹣8,0)
B.(0,8)
C.(0,8 ![]() )
)
D.(0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一根竹竿,不知道它有多长.把竹竿横放在一扇门前,竹竿长比门宽多4尺;把竹竿竖放在这扇门前,竹竿长比门的高度多2尺;把竹竿斜放,竹竿长正好和门的对角线等长.问竹竿长几尺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数y= ![]() 的图象经过点C,一次函数y=ax+b的图象经过点A、C,
的图象经过点C,一次函数y=ax+b的图象经过点A、C, 
(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成题目:
(1)如图(1),点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E在BC的延长线上,且CE=CP,连接BP,DE.求证:BP=DE且BP⊥DE;
(2)直线EP交AD于F,连接BF,FC.点G是FC与BP的交点.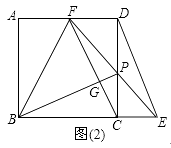
①若BC=2CE时,求证:BP⊥CF;
②若BC=nCE(n是大于1的实数)时,记△BPF的面积为S1 , △DPE的面积为S2 . 求证:S1=(n+1)S2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△ABC的三个顶点都在格点上,点A、C的坐标分别为(﹣2,4)、(﹣4,1),结合所给的平面直角坐标系解答下列问题: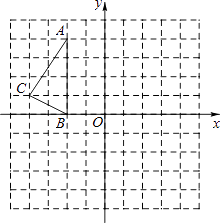
(1)点B的坐标是;
(2)在(1)的条件下,画出△ABC关于原点O对称的△A1B1C1 , 点A1坐标是;
(3)在(1)的条件下,平移△ABC,使点A移到点A2(0,2),画出平移后的△A2B2C2 , 点B2的坐标是 , 点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2013年“亚青会”,学校组织了一次游戏:每位选手朝特制的靶子上各投三次飞镖,在同一圆环内得分相同.如图所示,小明、小君、小红的成绩分别是29分、43分和33分,则小华的成绩是( )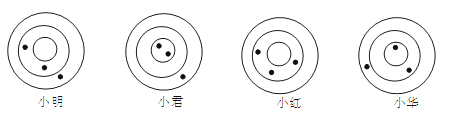
A.31分
B.33分
C.36分
D.38分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com