
如图,在直角坐标系中,矩形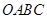 的顶点
的顶点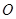 与坐标原点重合,顶点
与坐标原点重合,顶点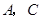 在坐标轴上,
在坐标轴上,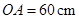 ,
,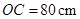 .动点
.动点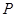 从点
从点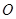 出发,以
出发,以 的速度沿
的速度沿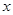 轴匀速向点
轴匀速向点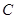 运动,到达点
运动,到达点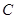 即停止.设点
即停止.设点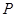 运动的时间为
运动的时间为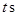 .
.
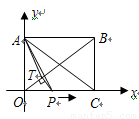
(1)过点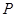 作对角线
作对角线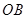 的垂线,垂足为点
的垂线,垂足为点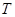 .求
.求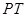 的长
的长 与时间
与时间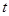 的函数关系式,并写出自变量
的函数关系式,并写出自变量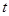 的取值范围;
的取值范围;
(2)在点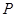 运动过程中,当点
运动过程中,当点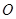 关于直线
关于直线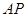 的对称点
的对称点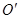 恰好落在对角线
恰好落在对角线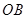 上时,求此时直线
上时,求此时直线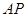 的函数解析式;
的函数解析式;
(3)探索:以 三点为顶点的
三点为顶点的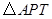 的面积能否达到矩形
的面积能否达到矩形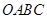 面积的
面积的 ?请说明理由.
?请说明理由.
(1)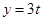 ,
,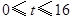 (2)
(2)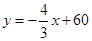 (3)不能,理由见解析
(3)不能,理由见解析
【解析】解:(1)在矩形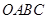 中,
中,
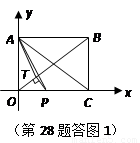
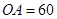 ,
,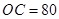 ,
,
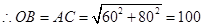 .……………………1分
.……………………1分
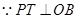 ,
,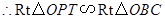 .
.
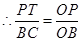 ,即
,即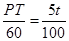 ,
,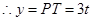 .……3分
.……3分
当点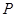 运动到
运动到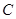 点时即停止运动,此时
点时即停止运动,此时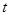 的最大值为
的最大值为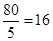 .
.
所以,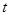 的取值范围是
的取值范围是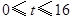 .················ 4分
.················ 4分
(2)当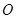 点关于直线
点关于直线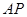 的对称点
的对称点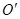 恰好在对角线
恰好在对角线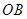 上时,
上时,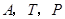 三点应在一条直线上(如答图2).……………………5分
三点应在一条直线上(如答图2).……………………5分
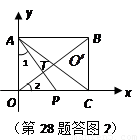
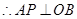 ,
,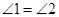 .
.
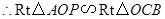 ,
,
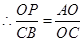 .
.
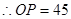 .
. 点
点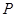 的坐标为
的坐标为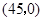 .…………6分
.…………6分
设直线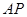 的函数解析式为
的函数解析式为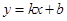 .将点
.将点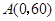 和点
和点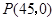 代入解析式,得
代入解析式,得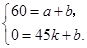 解这个方程组,得
解这个方程组,得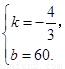
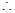 此时直线
此时直线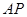 的函数解析式是
的函数解析式是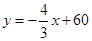 .········· 8分
.········· 8分
(3)由(2)知,当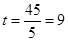 时,
时,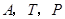 三点在一条直线上,此时点
三点在一条直线上,此时点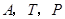 不构成三角形.
不构成三角形.
故分两种情况:
(i)当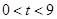 时,点
时,点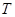 位于
位于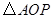 的内部(如答图3).
的内部(如答图3).
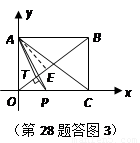
过 点作
点作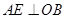 ,垂足为点
,垂足为点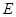 ,由
,由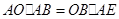
可得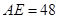 .
.
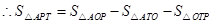
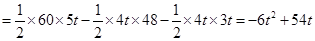 .······· 10分
.······· 10分
若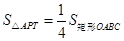 ,则应有
,则应有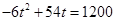 ,即
,即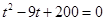 .
.
此时,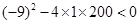 ,所以该方程无实数根.
,所以该方程无实数根.
所以,当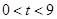 时,以
时,以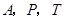 为顶点的
为顶点的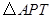 的面积不能达到矩形
的面积不能达到矩形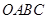 面积的
面积的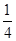 . 11分
. 11分
(ii)当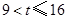 时,点
时,点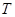 位于
位于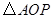 的外部.(如答图4)
的外部.(如答图4)
此时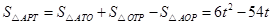 .········ 12分
.········ 12分
若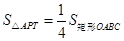 ,则应有
,则应有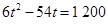 ,即
,即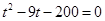 .
.
解这个方程,得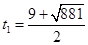 ,
,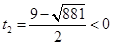 (舍去).
(舍去).
由于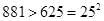 ,
,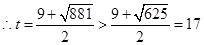 .
.
而此时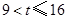 ,所以
,所以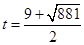 也不符合题意,故舍去.
也不符合题意,故舍去.
所以,当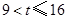 时,以
时,以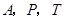 为顶点的
为顶点的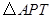 的面积也不能达到矩形
的面积也不能达到矩形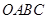 面积的
面积的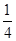 .
.
综上所述,以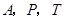 为顶点的
为顶点的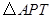 的面积不能达到矩形
的面积不能达到矩形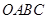 面积的
面积的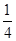 .
.
(1)找出三角形相似的条件,利用相似三角形的对应边成比例,求出边界值即可
(2)用待定系数法,找出直线上两点坐标即可,由于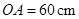 ,则
,则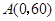 ,利用相似三角形的对应边成比例,求出点P的坐标
,利用相似三角形的对应边成比例,求出点P的坐标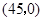
(3)由于点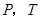 是动点,以
是动点,以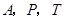 为顶点的
为顶点的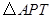 的面积与点
的面积与点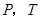 的位置有关,需分情况讨论,当
的位置有关,需分情况讨论,当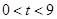 时,找不到
时,找不到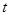 的值使得
的值使得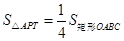 ,当
,当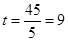 时,
时,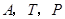 三点在一条直线上,则点
三点在一条直线上,则点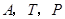 不构成三角形,当
不构成三角形,当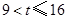 时,也找不到
时,也找不到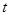 的值使得
的值使得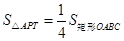 ,因此以
,因此以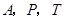 为顶点的
为顶点的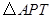 的面积不能达到矩形
的面积不能达到矩形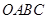 面积的
面积的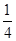


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′. | PP′ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 6 |
| x |
| 3 |
| 2 |
| 6 |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:
 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com