
如图,在等边三角形ABC中,BC=6 ,射线AG∥BC,点E从点A出发沿射线AG以
,射线AG∥BC,点E从点A出发沿射线AG以 的速度运动,同时点F从点B出发沿射线BC以
的速度运动,同时点F从点B出发沿射线BC以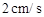 的速度运动,设运动时间为
的速度运动,设运动时间为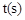
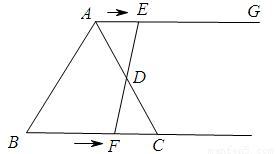
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF
(2)填空:
①当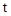 为 s时,四边形ACFE是菱形;
为 s时,四边形ACFE是菱形;
②当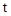 为 s时,以A,F,C,E为顶点的四边形是直角梯形。
为 s时,以A,F,C,E为顶点的四边形是直角梯形。
(1)见解析(2)①6 ②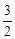
【解析】解:(1)证明:∵AG∥BC,∴∠EAD=∠ACB。
∵D是AC边的中点,∴AD=CD。
又∵∠ADE=∠CDF ,∴△ADE≌△CDF(ASA)。
(2)①6。
②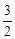 。
。
(1)由ASA证明△ADE≌△CDF。
(2)①∵当四边形ACFE是菱形时,∴AE=AC=CF=EF。
由题意可知:AE=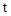 ,CF=
,CF=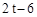 ,∴
,∴ ,即
,即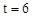 。
。
②若EF⊥AG,四边形ACFE是直角梯形,
过C作CM⊥AG于点M,

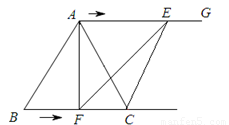
∵AM=3,AE=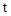 ,ME=CF=
,ME=CF=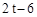 ,
,
∴AE-ME=AM,,即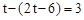 ,
,
此时,G与F重合,不符合题意,舍去。
若AF⊥BV,四边形若四边形AFCE是直角梯形,
∵△ABC是等边三角形,F是BC中点,
∴ ,解得
,解得 。
。
经检验,符合题意。


科目:初中数学 来源: 题型:
 如图,在等边三角形△ABC中,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,且PR=PS,下面给出的四个结论:①点P在∠A的平分线上,②AS=AR,③QP∥AR,④△BRP≌△QSP,则其中正确的是( )
如图,在等边三角形△ABC中,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,且PR=PS,下面给出的四个结论:①点P在∠A的平分线上,②AS=AR,③QP∥AR,④△BRP≌△QSP,则其中正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com