
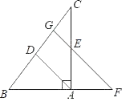
【题目】如图,在Rt△ABC中,∠BAC=90°,AD平分∠BAC,过AC的中点E作FG∥AD,交BA的延长线于点F,交BC于点G,
(1)求证:AE=AF;
(2)若BC=![]() AB,AF=3,求BC的长.
AB,AF=3,求BC的长.
【答案】(1)见解析;(2)BC=![]() .
.
【解析】
(1)由∠BAC=90°,AD平分∠BAC,得∠DAB=45°,又FG∥AD所以∠F=∠DAB=45°,∠AEF=45°,所以∠F=∠AEF,因此AE=AF;(2)由AF=3,AE=3,AC=2AE=6,在Rt△ABC中,AB2+AC2=BC2,求出AB=![]() ,因此BC=
,因此BC=![]() .
.
(1)∵∠BAC=90°,AD平分∠BAC,
∴∠DAB=![]() ∠CAB=
∠CAB=![]() ×90°=45°,
×90°=45°,
∵FG∥AD
∴∠F=∠DAB=45°,∠AEF=45°,
∴∠F=∠AEF,
∴AE=AF;
(2)∵AF=3,
∴AE=3,
∵点E是AC的中点,
∴AC=2AE=6,
在Rt△ABC中,AB2+AC2=BC2,
∴AB2+32=(![]() )2,
)2,
解得AB=![]() ,
,
∴BC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;

查看答案和解析>>
科目:初中数学 来源: 题型:
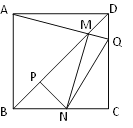
【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?”
设每只雀重x斤,每只燕重y斤,可列方程组为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
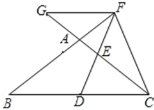
【题目】如图,在△ABC 中,AB =AC,点D在BC上,点F在BA的延长线上,FD =FC,点E是AC与DF的交点,且ED =EF,FG∥BC交CA的延长线于点G.
(1)∠BFD =∠GCF 吗?说明理由;
(2)求证:△GEF ≌△CED;
(3)求证:BD =DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
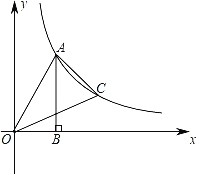
【题目】如图,点A是反比例函数y=![]() (x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB=
(x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB=![]() .点C是反比例函数y=
.点C是反比例函数y=![]() (x>0)图象上一动点,连接AC,OC,若△AOC的面积为
(x>0)图象上一动点,连接AC,OC,若△AOC的面积为![]() ,则点C的坐标为_____.
,则点C的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学抽取了40 名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
组别 | 时间/小时 | 频数 /人数 |
A组 |
| 2 |
B组 |
| m |
C组 |
| 10 |
D组 |
| 12 |
E组 |
| 7 |
F组 |
| 4 |

(1)求频数分布表中的m的值
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全统计图.
(3) 已知 该校有2000名学生,请你估计该校平均每周课外阅读时间在![]() 范围内的学生人数
范围内的学生人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com