
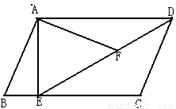
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
1.求证:∠DAF=∠CDE
2.问△ADF与△DEC相似吗?为什么?
3.若AB=4,AD=3 ,AE=3,求AF的长.
,AE=3,求AF的长.
1.见解析。
2.△ADF与△DEC相似
3.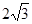
【解析】(1)∵平行四边形ABCD∴AB∥CD∴∠B+∠C=180°;又∵∠B=∠AFE ∴∠C=∠AFD;
又∵∠DAF+∠AFD+∠ADF=180°; ∠CDE+∠C+∠ADF=180°;∴∠DAF=∠CDE
(2) △ADF与△DEC相似 ∵四边形ABCD是平行四边形 ∴AD∥BC AB∥CD ∴∠ADF=∠CED
∠B+∠C=180° ∵∠AFE+∠AFD=180°∠AFE=∠B ∴∠AFD=∠C ∴△ADF∽△DEC
(3)解:∵四边形ABCD是平行四边形
∴AD∥BC CD=AB=4 又∵AE⊥BC ∴ AE⊥AD
在Rt△ADE中,DE=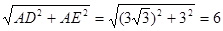
∵△ADF∽△DEC ∴ 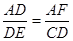 ∴
∴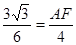 AF=
AF=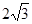


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2| 2 |
| 3 |
| 5 |
| A、AC⊥BD |
| B、四边形ABCD是菱形 |
| C、△ABO≌△CBO |
| D、AC=BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com