
【题目】如图,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
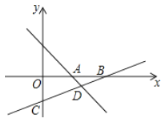
![]() 求直线
求直线![]() 的函数关系式;
的函数关系式;
![]() 点
点![]() 是
是![]() 上的一点,若
上的一点,若![]() 的面积等于
的面积等于![]() 的面积的
的面积的![]() 倍,求点
倍,求点![]() 的坐标.
的坐标.
![]() 设点
设点![]() 的坐标为
的坐标为![]() ,是否存在
,是否存在![]() 的值使得
的值使得![]() 最小?若存在,请求出点
最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x-2;(2)(
x-2;(2)(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)(
);(3)(![]() ,3).
,3).
【解析】
(1)把点(3,-1),点B(6,0)代入直线l2,求出k、b的值即可;
(2)设点P的坐标为(t,![]() t-2),求出D点坐标,再由S△ABP=2S△ABD求出t的值即可;
t-2),求出D点坐标,再由S△ABP=2S△ABD求出t的值即可;
(3)作直线y=3,作点A关于直线y=3的对称点A′,连结A′B,利用待定系数法求出其解析式,根据点Q(m,3)在直线A′B上求出m的值,进而可得出结论.
解:(1)由题知:
![]()
解得:
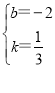 ,
,
故直线l2的函数关系式为:y=![]() x-2;
x-2;
(2)由题及(1)可设点P的坐标为(t,![]() t-2).
t-2).
解方程组 ,得
,得 ,
,
∴点D的坐标为(![]() ,-
,-![]() ).
).
∵S△ABP=2S△ABD,
∴![]() AB|
AB|![]() t-2|=2×
t-2|=2×![]() AB|-
AB|-![]() |,即|
|,即|![]() t-2|=
t-2|=![]() ,解得:t=
,解得:t=![]() 或t=
或t=![]() ,
,
∴点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)作直线y=3(如图),再作点A关于直线y=3的对称点A′,连结A′B.
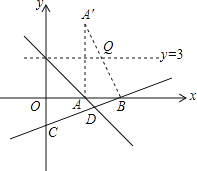
由几何知识可知:A′B与直线y=3的交点即为QA+QB最小时的点Q.
∵点A(3,0),
∴A′(3,6)
∵点B(6,0),
∴直线A′B的函数表达式为y=-2x+12.
∵点Q(m,3)在直线A′B上,
∴3=-2m+12
解得:m=![]() ,
,
故存在m的值使得QA+QB最小,此时点Q的坐标为(![]() ,3).
,3).


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,函数y=x的图象与函数y![]() 的图象相交于点P(1,m).
的图象相交于点P(1,m).
(1)求 m,k 的值.
(2)直线 y=2与函数y=x的图象相交于点A,与函数y![]() 的图象相交于点B,求线段 AB 长.
的图象相交于点B,求线段 AB 长.
(3)直接写出不等式x![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
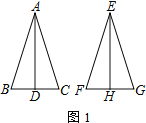
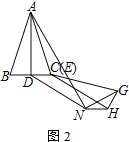
【题目】如图1,AB=AC,EF=EG,△ABC≌△EFG,AD⊥BC于点D,EH⊥FG于点H
(1) 直接写出AD、EH的数量关系:___________________
(2) 将△EFG沿EH剪开,让点E和点C重合
① 按图2放置△EHG,将线段CD沿EH平移至HN,连接AN、GN,求证:AN⊥GN
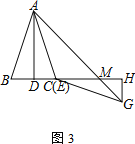
② 按图3放置△EHG,B、C(E)、H三点共线,连接AG交EH于点M.若BD=1,AD=3,求CM的长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是该直线上的一个动点.
是该直线上的一个动点.
(1)![]() ________;
________;![]() 的坐标为__________;
的坐标为__________;
(2)若点![]() 在第二象限内运动,试写出
在第二象限内运动,试写出![]() 的面积
的面积![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(3)探究:若点![]() 在该直线上任意运动,当
在该直线上任意运动,当![]() 的面积为6时,点
的面积为6时,点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com