
分析 观察题中代数式可发现如果各项的系数都乘以2,则该式可整理成完全平方的形式,所以代数式可变形为a2+b2+c2+ab+bc-ac=$\frac{1}{2}$(2a2+2b2+2c2+2ab+2bc-2ac)=$\frac{1}{2}$[(a+b)2+(b+c)2+(a-c)2],再根据条件求出(a-c)的值代入即可求解.
解答 解:∵a+b=5①,b+c=2②
∴①-②得a-c=3
∴a2+b2+c2+ab+bc-ac
=$\frac{1}{2}$(2a2+2b2+2c2+2ab+2bc-2ac)
=$\frac{1}{2}$[(a+b)2+(b+c)2+(a-c)2]
=$\frac{1}{2}$(25+4+9)
=19.
点评 本题考查了因式分解的应用,化简求值是课程标准中所规定的一个基本内容,它涉及对运算的理解以及运算技能的掌握两个方面.本题要熟悉2a2+2b2+2c2+2ab+2bc-2ac=(a+b)2+(b+c)2+(a-c)2,灵活运用并利用整体代入的思想解题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标中,A为x轴上一点,过A点的直线L的解析式为y=kx-k(其中k为常数,且k≠0),B(3,m)为直线L上的另一点,C是y轴上一动点,过C点作直线L的平行线L′,连结AC,过B点作BD∥AC交于L′于D点.
在平面直角坐标中,A为x轴上一点,过A点的直线L的解析式为y=kx-k(其中k为常数,且k≠0),B(3,m)为直线L上的另一点,C是y轴上一动点,过C点作直线L的平行线L′,连结AC,过B点作BD∥AC交于L′于D点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-2,1),B(1,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
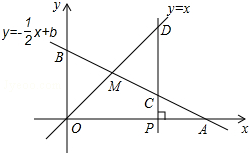 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个函数图象都经过第四象限 | |
| B. | 两个函数图象有两个公共点 | |
| C. | 两个函数在自变量的取值范围内y都随x的增大而增大 | |
| D. | 在第二象限内,函数y=x+1的值小于函数y=-$\frac{1}{x}$的值 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
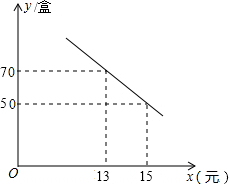 某种鲜花的成本价为每盆12元,在销售中每盆鲜花售价x(单位:元)与每日销售量y(单位:盆)之间的函数关系如图所示.
某种鲜花的成本价为每盆12元,在销售中每盆鲜花售价x(单位:元)与每日销售量y(单位:盆)之间的函数关系如图所示. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com