
【题目】如图,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,若已知
,若已知![]() 点的坐标为
点的坐标为![]() .
.
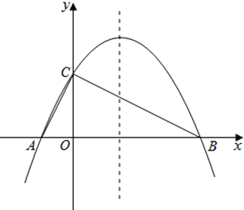
(1)求抛物线的解析式;
(2)求线段![]() 所在直线的解析式;
所在直线的解析式;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,求出符合条件的
为等腰三角形?若存在,求出符合条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,(2,2)或(2,-2)或(2,0)或(2,
;(3)存在,(2,2)或(2,-2)或(2,0)或(2,![]() )
)
【解析】
(1)将A点代入抛物线的解析式即可求得答案;
(2)先求得点B、点C的坐标,利用待定系数法即可求得直线BC的解析式;
(3)设出P点坐标,然后表示出△ACP的三边长度,分三种情况计论,根据腰相等建立方程,求解即可.
(1)将点![]() 代入
代入![]() 中,
中,
得:![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)当![]() 时,
时,![]() ,
,
∴点C的坐标为(0,4) ,
当![]() 时,
时,![]() ,
,
解得:![]() ,
,
∴点B的坐标为(6,0) ,
设直线BC的解析式为![]() ,
,
将点B (6,0),点C (0,4)代入,得:
![]() ,
,
∴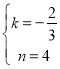 ,
,
∴直线BC的解析式为![]() ,
,
(3)抛物线的对称轴为![]() ,
,
假设存在点P,设![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
∵△ACP为等腰三角形,
①当![]() 时,
时,![]() ,
,
解之得:![]() ,
,
∴点P的坐标为(2,2)或(2,-2);
②当![]() 时,
时,![]() ,
,
解之得:![]() 或
或![]() (舍去),
(舍去),
∴点P的坐标为(2,0)或(2,8),
设直线AC的解析式为![]() ,
,
将点A(-2,0)、C (0,4)代入得![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴点(2,8)在直线AC上,
∴A、C、P在同一直线上,点(2,8)应舍去;
③当![]() 时,
时,![]() ,
,
解之得:![]() ,
,
∴点P的坐标为(2,![]() );
);
综上,符合条件的点P存在,坐标为:(2,2)或(2,-2)或(2,0)或(2,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() OABC的顶点A, C的坐标分别为A(2,0),C(-1,2),反比例函数
OABC的顶点A, C的坐标分别为A(2,0),C(-1,2),反比例函数![]() 的图像经过点B.
的图像经过点B.
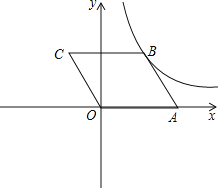
(1)求k的值.
(2)将![]() OABC沿着x轴翻折,点C落在点C′处.判断点C′是否在反比例函数
OABC沿着x轴翻折,点C落在点C′处.判断点C′是否在反比例函数![]() 的图像上,请通过计算说明理由.
的图像上,请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的高,点G、H在BC边上,点E在AB边上,点F在AC边上,BC=10cm,AD=8cm,四边形EFHG是矩形.
(1)△AEF与△ABC相似吗?请说明理由.
(2)若矩形EFHG的面积为15cm2,求这个矩形的长和宽.
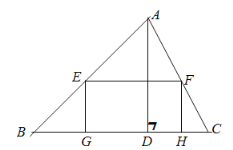
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50cm,拉杆BC的伸长距离最大时可达35cm,点A,B,C在同一条直线上,在箱体底端装有圆形的滚筒轮⊙A,⊙A与水平地面相切于点D,在拉杆伸长到最大的情况下,当点B距离水平地面34cm时,点C到水平地面的距离CE为55cm.设AF∥ MN.

(1)求⊙A的半径.
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为76cm,∠CAF=64°,求此时拉杆BC的伸长距离(结果精确到1cm,参考数据:sin64°≈0.9,cos64°≈0.39,tan64°≈2.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .分别以点
.分别以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 长为半径作弧,两弧交于点
长为半径作弧,两弧交于点![]() ,作直线
,作直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .请回答:
.请回答:
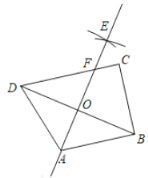
(1)直线![]() 与线段
与线段![]() 的关系是_______________.
的关系是_______________.
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了.
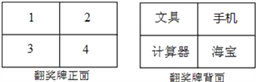
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
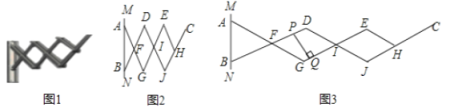
【题目】如图1是一个三节段式伸缩晾衣架,如图2,是其衣架侧面示意图.![]() 为衣架的墙体固定端,
为衣架的墙体固定端,![]() 为固定支点,
为固定支点,![]() 为滑动支点,四边形
为滑动支点,四边形![]() 和四边形
和四边形![]() 是菱形,且
是菱形,且![]() .点
.点![]() 在
在![]() 上滑动时,衣架外延钢体发生角度形变,其外延长度(点
上滑动时,衣架外延钢体发生角度形变,其外延长度(点![]() 和点
和点![]() 间的距离)也随之变化,形成衣架伸缩效果.伸缩衣架为初始状态时,衣架外延长度为42
间的距离)也随之变化,形成衣架伸缩效果.伸缩衣架为初始状态时,衣架外延长度为42![]() .当点
.当点![]()
![]() 向点
向点![]() 移动8
移动8![]() 时,外延长度为9
时,外延长度为9![]() .如图3,当外延长度为120
.如图3,当外延长度为120![]() 时,则
时,则![]() 和
和![]() 的间距
的间距![]() 长为_______.
长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
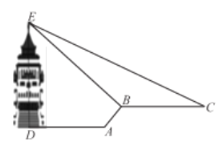
【题目】缙云山是国家级自然风景名胜区,上周周末,小明和妈妈到缙云山游玩,登上了香炉峰观景塔,从观景塔底中心![]() 处水平向前走
处水平向前走![]() 米到
米到![]() 点处,再沿着坡度为
点处,再沿着坡度为![]() 的斜坡
的斜坡![]() 走一段距离到达
走一段距离到达![]() 点,此时回望观景塔,更显气势宏伟,在
点,此时回望观景塔,更显气势宏伟,在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 再往前沿水平方向走
再往前沿水平方向走![]() 米到
米到![]() 处,观察到观景塔顶端的仰角是
处,观察到观景塔顶端的仰角是![]() ,则观景塔的高度
,则观景塔的高度![]() 为( )(tan22°≈0.4)
为( )(tan22°≈0.4)
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com