
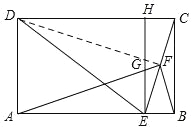
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 边上一点,
边上一点,![]() 平分
平分![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() 分别交
分别交![]() 于
于![]() ,
,![]() 两点.
两点.

(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当![]() 时,请直接写出
时,请直接写出![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)4![]() .
.
【解析】
试题分析:(1)根据平行线的性质以及角平分线的定义,即可得到∠DCE=∠DEC,进而得出DE=DC;
(2)连接DF,根据等腰三角形的性质得出∠DFC=90°,再根据直角三角形斜边上中线的性质得出BF=CF=EF=![]() EC,再根据SAS判定△ABF≌△DCF,即可得出∠AFB=∠DFC=90°,据此可得AF⊥BF;
EC,再根据SAS判定△ABF≌△DCF,即可得出∠AFB=∠DFC=90°,据此可得AF⊥BF;
(3)根据等角的余角相等可得∠BAF=∠FEH,再根据公共角∠EFG=∠AFE,即可判定△EFG∽△AFE,进而得出EF2=AFGF=28,求得EF=2![]() ,即可得到CE=2EF=4
,即可得到CE=2EF=4![]() .
.
试题解析:(1)∵四边形ABCD是矩形,∴AB∥CD,∴∠DCE=∠CEB,
∵EC平分∠DEB,∴∠DEC=∠CEB,∴∠DCE=∠DEC,∴DE=DC;
(2)如图,连接DF,
∵DE=DC,F为CE的中点,∴DF⊥EC,∴∠DFC=90°,
在矩形ABCD中,AB=DC,∠ABC=90°,∴BF=CF=EF=![]() EC,∴∠ABF=∠CEB,
EC,∴∠ABF=∠CEB,
∵∠DCE=∠CEB,∴∠ABF=∠DCF,
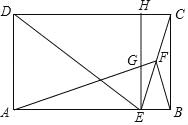
在△ABF和△DCF中,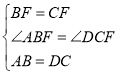 ,∴△ABF≌△DCF(SAS),∴∠AFB=∠DFC=90°,
,∴△ABF≌△DCF(SAS),∴∠AFB=∠DFC=90°,
∴AF⊥BF;
(3)CE=4![]() .
.
理由如下:∵AF⊥BF,∴∠BAF+∠ABF=90°,
∵EH∥BC,∠ABC=90°,∴∠BEH=90°,∴∠FEH+∠CEB=90°,
∵∠ABF=∠CEB,∴∠BAF=∠FEH,
∵∠EFG=∠AFE,∴△EFG∽△AFE,∴![]() ,即EF2=AFGF,
,即EF2=AFGF,
∵AFGF=28,∴EF=2![]() ,∴CE=2EF=4
,∴CE=2EF=4![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题满分6分)
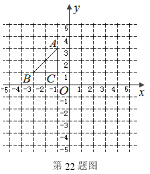
如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(-1,3),B(-3,1),C(-1,1).请解答下列问题:
⑴ 画出△ABC关于y轴对称的△A1B1C1,并写出B1的坐标.
⑵ 画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1,并求出点A1走过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,
,![]() 是抛物线的顶点.
是抛物线的顶点.
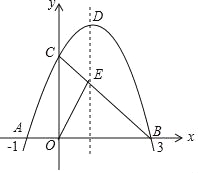
(1)求此抛物线的解析式;
(2)直接写出点![]() 和点
和点![]() 的坐标;
的坐标;
(3)若点![]() 在第一象限内的抛物线上,且
在第一象限内的抛物线上,且![]() ,求
,求![]() 点坐标.
点坐标.
注:二次函数![]() (
(![]() )的顶点坐标为
)的顶点坐标为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).
A.中位数B.众数C.平均数D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com