
【题目】如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=b,移在动过程中,双曲线y=![]() (x>0)的图象始终经过BC的中点E,交AB于点D.
(x>0)的图象始终经过BC的中点E,交AB于点D.
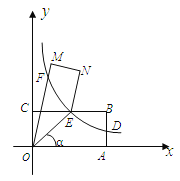
(1)证明:点D是AB的中点;
(2) 连结OE记∠AOE= α.
①当α=45°时,求 a、b之间的数量关系;
②当α=30°,k=![]() 时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
形OMNE除点E外的另一个交点为F,求直线DF的解析式
【答案】(1)见解析 (2)① a=2b ②![]()
【解析】分析:(1)根据中点坐标公式得到E点坐标,再根据待定系数法得到双曲线解析式,把D点的横坐标代入可求D点的纵坐标,依此即可证明;
(2)①根据等腰直角三角形的性质即可得到a、b之间的数量关系;
②首先过点E作EH⊥OA于点H,过点F作FG⊥OA于点G,由∠EOA=30°,k=![]() ,即可求得点E的坐标,又由点E是BC的中点,可求得点D的横坐标,继而求得点D的坐标,然后由折叠的性质,可得∠FOA=60°,即可求得点F的坐标,然后由待定系数法求得直线DF的解析式.
,即可求得点E的坐标,又由点E是BC的中点,可求得点D的横坐标,继而求得点D的坐标,然后由折叠的性质,可得∠FOA=60°,即可求得点F的坐标,然后由待定系数法求得直线DF的解析式.
详解: ![]() ,
,
![]() ,
,
![]() ,得:
,得:![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() (3)如图,过点E作EH⊥OA于点H,过点F作FG⊥OA于点G,
(3)如图,过点E作EH⊥OA于点H,过点F作FG⊥OA于点G,
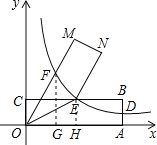
∵∠AOE=30°,k=![]() ,
,
∴![]() =
=![]() ,
,
∴OH=![]() EH,
EH,
∵S△EOH=![]() OHEH=
OHEH=![]() k=
k=![]() ,
,
∴EH=1,OH=![]() ,
,
∵E是BC的中点,
∴OA=2OH=2![]() ,
,
∴点D的横坐标为2![]() ,
,
则y=![]() ,
,
∴点D(2![]() ,
,![]() ),
),
由折叠的性质可得:∠FOA=2∠AOE=60°,
∴FG:OG=![]() ,
,
∵S△FOG=![]() OGFG=
OGFG=![]() k═
k═![]() ,
,
∴OG=1,FG=![]() ,
,
∴点F(1,![]() ),
),
设直线EF的解析式为:y=ax+b,
则 ,
,
解得: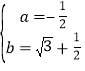 ,
,
∴直线EF的解析式为:y=![]() x+
x+![]() +
+![]() .
.


科目:初中数学 来源: 题型:
【题目】请阅读求绝对值不等式|x|<3和|x|>3的解集的过程:
因为|x|<3,从如图1所示的数轴上看:大于-3而小于3的数的绝对值是小于3的,所以|x|<3的解集是-3<x<3;
因为|x|>3,从如图2所示的数轴上看:小大于-3的数和大于3的数的绝对值是大于3的,所以|x|>3的解集是x<-3或x>3.
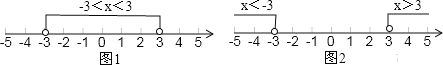
解答下面的问题:
(1)不等式|x|<a(a>0)的解集为______;不等式|x|>a(a>0)的解集为______.
(2)解不等式|x-5|<3;
(3)解不等式|x-3|>5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 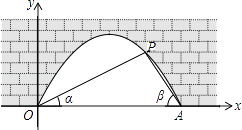
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
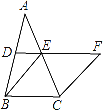
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电动车厂平均每天计划生产200辆电动车,由于各种原因实际每天的生产量与计划量相比有出入.下表是某周的生产情况(超产为正,减产为负)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减情况 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(1)产量最多的一天比产量最少的一天多生产多少辆?
(2)根据记录可知前五天共生产多少辆?
(3)该厂实行计件工资制,每辆车100元,超额完成则超额部分每辆车再奖励40元(以一周为单位结算),那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图![]() 所示,点
所示,点![]() 为矩形
为矩形![]() 边
边![]() 的中点,在矩形
的中点,在矩形![]() 的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员
的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路线匀速行进,到达点
的路线匀速行进,到达点![]() .设运动员
.设运动员![]() 的运动时间为
的运动时间为![]() ,到监测点的距离为
,到监测点的距离为![]() .现有
.现有![]() 与
与![]() 的函数关系的图象大致如图
的函数关系的图象大致如图![]() 所示,则这一信息的来源是( ).
所示,则这一信息的来源是( ).
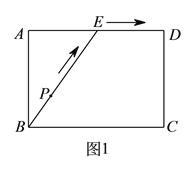

A. 监测点![]() B. 监测点
B. 监测点![]() C. 监测点
C. 监测点![]() D. 监测点
D. 监测点![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
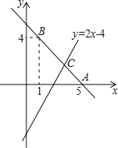
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB= ![]() ,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.
,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F. 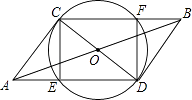
(1)问四边形CEDF是何种特殊四边形?请证明你的结论;
(2)当AC与⊙O相切时,四边形CEDF是正方形吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t= . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com