
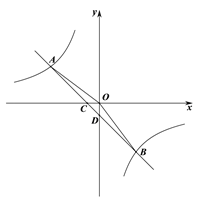
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数图象交于第二,四象限内A,B两点,与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于点D.若点B的纵坐标为
轴交于点D.若点B的纵坐标为![]() ,OA=5,
,OA=5, ![]() .
.
(1)求反比例函数解析式;
(2)求△AOB的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1))过点A作![]() 轴于E,设反比例函数解析式为
轴于E,设反比例函数解析式为![]() ,通过解直角三角形求出线段AE、OE的长度,即求出点A的坐标;再由点A的坐标利用待定系数法求出反比例函数解析式即可;
,通过解直角三角形求出线段AE、OE的长度,即求出点A的坐标;再由点A的坐标利用待定系数法求出反比例函数解析式即可;
(2)由点B在反比例函数图象上可求出点B的坐标,求出直线AB的解析式,再令该解析式中y=0即可求出点C的坐标,再利用三角形的面积公式即可得出结论.
详解:(1)过点A作![]() 轴于E,
轴于E,
∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点A的坐标为![]()
设所求反比例函数解析式为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴所求反比例函数解析式为![]() .
.
(2)∵在![]() 中,当
中,当![]() 时,
时, ![]() ,
,
∴点B的坐标为![]() ,
,
由A![]() ,B
,B![]() 可得AB所在直线为:
可得AB所在直线为: ![]() ,
,
∵在上式中当![]() 时,
时, ![]() ,
,
∴点D的坐标为![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() .
.


科目:初中数学 来源: 题型:
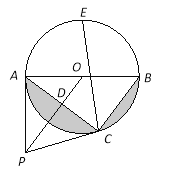
【题目】如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是弧AB的中点,连接CE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年11月9日,微信团队在成都腾讯全球合作伙伴大会上发布消息称:2017年全球平均日登录微信用户数9.02亿,较去年增长17%.按此增长速度,预计2019年全球平均日登录微信用户数为( )
A. 9.02×(17%)2亿 B. 9.02×(1+17%)亿 C. 9.02×(1+17%)2亿 D. 9.02×(1+2×17%)亿
查看答案和解析>>
科目:初中数学 来源: 题型:
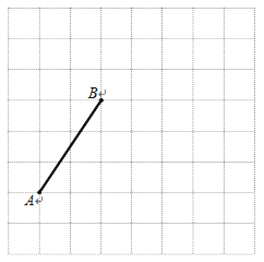
【题目】下图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.
(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(-3,-1),在此坐标系下,B点的坐标为________________;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为__________________;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c(a≠0)的图象过O、B、C三点,则此函数图象的对称轴方程是________________.
【答案】 (-1,2) (2,0) x=1
【解析】分析:![]() 根据点
根据点![]() 的坐标建立坐标系,即可写出点
的坐标建立坐标系,即可写出点![]() 的坐标.
的坐标.
![]() 画出点
画出点![]() 旋转后的对应点
旋转后的对应点![]() 连接
连接![]() ,写出点
,写出点![]() 的坐标.
的坐标.
![]() 用待定系数法求出函数解析式,即可求出对称轴方程.
用待定系数法求出函数解析式,即可求出对称轴方程.
详解:(1)建立坐标系如图,
B点的坐标为![]() ;
;
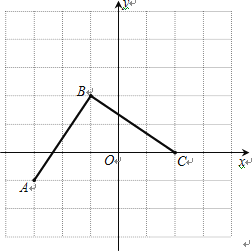
(2)线段BC如图,C点的坐标为![]()
(3)把点![]() 代入二次函数
代入二次函数![]() ,得
,得
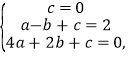
解得: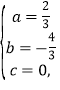
二次函数解析为:![]()
对称轴方程为:![]()
故对称轴方程是![]()
点睛:考查图形与坐标;旋转、对称变换;待定系数法求二次函数解析式,二次函数的图象与性质.熟练掌握各个知识点是解题的关键.
【题型】解答题
【结束】
18
【题目】特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2021,61×69=4209.
(1)请你直接写出83×87的值;
(2)设这两个两位数的十位数字为x(x>3),个位数字分别为y和z(y+z=10),通过计算验证这两个两位数的乘积为100x(x+1)+yz.
(3)99991×99999=___________________(直接填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
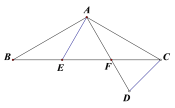
(1)求证:ΔABE≌ΔACF;
(2)若∠BAE=30°,则∠ADC= (直接写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点![]() 、
、![]() 表示的有理数分别为-10、5,点
表示的有理数分别为-10、5,点![]() 是射线
是射线![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合),点
重合),点![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点,点
的三等分点,点![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点.
的三等分点.
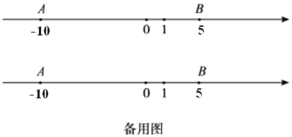
(1)若点![]() 表示的有理数是0,那么
表示的有理数是0,那么![]() 的长为______;若点
的长为______;若点![]() 表示的有理数是1,那么
表示的有理数是1,那么![]() 的长为______.
的长为______.
(2)点![]() 在射线
在射线![]() 上运动(不与点
上运动(不与点![]() 、
、![]() 重合)的过程中,
重合)的过程中,![]() 的长是否发生改变?若不改变,请求出
的长是否发生改变?若不改变,请求出![]() 的长;若改变,请说明理由.
的长;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
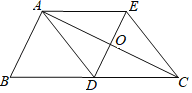
【题目】如图,已知△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
(1)求证:四边形ADCE是平行四边形;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com