
【题目】林华在2018年共两次到某商场按照标价购买了A,B两种商品,其购买情况如下表:
购买A商品的数量(个) | 购买B商品的数量(个) | 购买两种商品的总费用(元) | |
第一次购买 | 6 | 5 | 1140 |
第二次购买 | 3 | 7 | 1110 |
(1)分别求出A、B两种商品的标价。
(2)最近商场实行“迎2019新春”的促销活动,A,B两种商品都打折且折扣数相同,于是林华前往商场花1062元又购买了9个A商品和8个B商品,试问本次促销活动中A,B商品的折扣数都为多少?在本次购买中,林华共节约了多少钱?
【答案】(1)A种商品标价90元,B种商品标价120元;(2)两种商品打6折出售,共节约708元
【解析】
(1)设商品A的标价为x元/个,商品B的标价为y元/个,根据总价=单价×数量结合前两次购买商品的数量及费用,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)根据折扣率=现价÷原价×10,即可求出结论.
(1)设A种商品标价x元,B种商品标价y元,则
![]() ,
,
解得![]() .
.
∴A种商品标价90元,B种商品标价120元;
(2)设商店是打a折出售的这两种产品,根据题意得
(9×90+8×120) ×![]() =1062,
=1062,
解得a=6,
故商店是打6折出售的这两种产品.
林华节省了9×90+8×120-1062=708(元).


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )
A.![]()
B.![]()
C.π
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
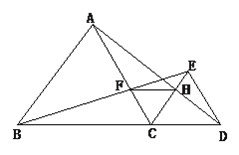
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在△ABC的内部且DB=DC,点E,F在△ABC的外部,FB=FA,EA=EC,∠FBA=∠DBC=∠ECA.
(1)①填空:△ACE∽∽;
(2)求证:△CDE∽△CBA;
(3)求证:△FBD≌△EDC;
(4)若点D在∠BAC的平分线上,判断四边形AFDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(0,6)的抛物线y= ![]() x2+bx+c与x轴相交于B(﹣2,0)、C两点.
x2+bx+c与x轴相交于B(﹣2,0)、C两点.
(1)求此抛物线的函数关系式和顶点D的坐标;
(2)求直线AC所对应的函数关系式;
(3)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1 , 若新抛物线y1的顶点P在△ABC内,求m的取值范围;
(4)在(3)的结论下,新抛物线y1上是否存在点Q,使得△QAB是以AB为底边的等腰三角形,请分析所有可能出现的情况,并直接写出相对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
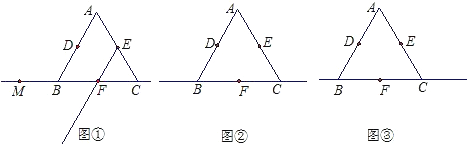
【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?不要求证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com