Question

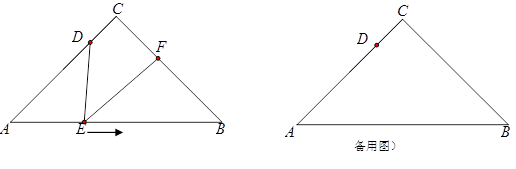
（12分）如图，在Rt△ABC中，∠C=90°，AC=BC=4cm，点D为AC边上一

点，且AD=3cm，动点E从点A出发，以1cm/s的速度沿线段AB向终点B运动，运动

时间为x s．作∠DEF=45°，与边BC相交于点F．设BF长为ycm．

（1）当x=   ▲  s时，DE⊥AB；

（2）求在点E运动过程中，y与x之间的函数关系式及点F运动路线的长；

（3）当△BEF为等腰三角形时，求x的值．

 

Answer 1

解：（1）······················································································· 2分

   （2）∵在△ABC中，∠C=90°，AC=BC=4．

∴∠A＝∠B＝45°，AB=4，∴∠ADE＋∠AED＝135°；

又∵∠DEF＝45°，∴∠BEF＋∠AED＝135°，∴∠ADE＝∠BEF；

∴△ADE∽△BEF····················································································· 4分

∴＝，

（3）这里有三种情况：

①如图，若EF＝BF，则∠B＝∠BEF；

又∵△ADE∽△BEF，∴∠A＝∠ADE＝45°

∴∠AED＝90°，∴AE＝DE＝，

 

∵动点E的速度为1cm/s ，∴此时x＝s；

②如图，若EF＝BE，则∠B＝∠EFB

 

又∵△ADE∽△BEF，∴∠A＝∠AED＝45°

∴∠ADE＝90°，∴AE＝3，

∵动点E的速度为1cm/s

∴此时x＝3s；

③如图，若BF＝BE，则∠FEB＝∠EFB；

 

又∵△ADE∽△BEF，∴∠ADE＝∠AED

∴AE＝AD＝3，

∵动点E的速度为1cm/s

∴此时x＝3s；

综上所述，当△BEF为等腰三角形时，x的值为s或3s或3s．

 

（注：求对一个结论得2分，求对两个结论得4分，求对三个结论得5分）

解析:略