已知四边形ABCD,AD∥BC,连接BD.
(1)小明说:“若添加条件BD2=BC2+CD2,则四边形ABCD是矩形.”你认为小明的说法是否正确?若正确,请说明理由;若不正确,请举出一个反例说明;
(2)若BD平分∠ABC,∠DBC=∠BDC,tan∠DBC=1,求证:四边形ABCD是正方形.
【答案】
分析:(1)根据题意作出(直角)梯形ABCD,使得AD∥BC,且∠C=90°,则四边形ABCD是直角梯形不是矩形;
(2)根据tan∠DBC=1,BD平分∠ABC,∠DBC=∠BDC求出四边形ABCD是正方形.
解答: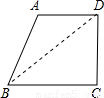
(1)解:不正确.(1分)
如图作(直角)梯形ABCD,(2分)
使得AD∥BC,∠C=90°.
连接BD,则有BD
2=BC
2+CD
2.(3分)
而四边形ABCD是直角梯形不是矩形.(4分)
(2)证明:如图,
∵tan∠DBC=1,
∴∠DBC=45°.(5分)
∵∠DBC=∠BDC,
∴∠BDC=45°.
且BC=DC.(6分)
法1:∵BD平分∠ABC,
∴∠ABD=45°,∴∠ABD=∠BDC.
∴AB∥DC.
∴四边形ABCD是平行四边形.(7分)
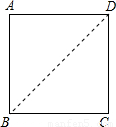
又∵∠ABC=45°+45°=90°,
∴四边形ABCD是矩形.(8分)
∵BC=DC,
∴四边形ABCD是正方形.(9分)
法2:∵BD平分∠ABC,∠BDC=45°,∴∠ABC=90°.
∵∠DBC=∠BDC=45°,∴∠BCD=90°.
∵AD∥BC,
∴∠ADC=90°.(7分)
∴四边形ABCD是矩形.(8分)
又∵BC=DC
∴四边形ABCD是正方形.(9分)
法3:∵BD平分∠ABC,∴∠ABD=45°.∴∠BDC=∠ABD.
∵AD∥BC,∴∠ADB=∠DBC.
∵BD=BD,
∴△ADB≌△CBD.
∴AD=BC=DC=AB.(7分)
∴四边形ABCD是菱形.(8分)
又∵∠ABC=45°+45°=90°,
∴四边形ABCD是正方形.(9分)
点评:本题比较新颖,考查了学生对所学知识的综合运用能力,及创新能力,是中考的热点.

 (1)解:不正确.(1分)
(1)解:不正确.(1分)


 名校课堂系列答案
名校课堂系列答案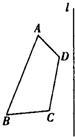 32、如图,已知四边形ABCD和直线L.
32、如图,已知四边形ABCD和直线L.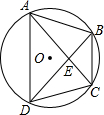 如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )
如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )
