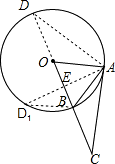
(1)解:AC与⊙O相切.(1分)
证明:如图,∵AB与半径相等,即AB=OA=OB,
∴△OAB为等边三角形,
∴∠OAB=60°,∠OBA=60°.
∵BC=OB=AB,
∴∠BAC=∠C=30°,
∴∠OAC=90°,(2分)
∴AC与⊙O相切.
(2)延长BO交⊙O于D,连接AD,则必有AD=AC.(3分)
证明:∵∠BOA=60°,OA=OD,
∴∠D=30°.
又∵∠C=30°,
∴∠C=∠D,
∴AD=AC.(4分)
∵△OAB为等边三角形,
∴∠ABD=60°.(5分)
或作AD
1⊥OC交⊙O于D
1,交OC于E,连接BD
1,则必有AD
1=AC.(3分)
证明:∵∠C=30°,AD
1⊥OC,
∴AE=

AC.
又∵AE=

AD
1,
∴AC=AD
1.(4分)
由OE⊥AD1,得到

=
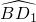
,
∴∠BAD
1=∠BD
1A=

∠AOB=30°,
∴∠ABD
1=120°.(5分)
分析:(1)由线段AB与两半径的相等得出三角形AOB为等边三角形,根据等边三角形的性质可知∠OAB和∠OBA都为60度,根据等边对等角及外角的性质可得出∠BAC=30°,进而得到∠OAC=90°,由OA是圆的半径,即可得到AC是圆的切线;
(2)分两种情况考虑:延长BO交⊙O于D,连接AD,则必有AD=AC,原因为:根据同弧所对的圆周角等于圆心角的一半,得到∠D=30°,进而得到∠D与∠C相等,根据等角对等边得到AD=AC,求出此时∠ABD的度数;作AD
1⊥OC交⊙O于D
1,交OC于E,连接BD
1,则必有AD
1=AC.原因为:在直角三角形ACE中,根据30°角所对的直角边等于斜边的一半得到AE等于AC的一半,再根据垂径定理得到AE等于AD
1的一半,故AC与AD
1相等,求出此时∠ABD的度数.
点评:本题考查切线的性质和判定及圆周角定理的综合运用,考查了分类讨论的数学思想.学生在作第二问时应注意审清题意,画出图形,然后分类作答.

 如图,在⊙O中,弦AB与半径相等,连接OB并延长,使BC=OB.
如图,在⊙O中,弦AB与半径相等,连接OB并延长,使BC=OB. (1)解:AC与⊙O相切.(1分)
(1)解:AC与⊙O相切.(1分) AC.
AC. AD1,
AD1, =
=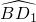 ,
, ∠AOB=30°,
∠AOB=30°,

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案 标系.
标系.