
【题目】如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且 ![]() =
= ![]() .
. 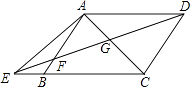
(1)求证:AB∥CD;
(2)如果AD2=DGDE,求证: ![]() =
= ![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2 ![]() ,E为CD的中点,点F在线段PB上.
,E为CD的中点,点F在线段PB上. 
(Ⅰ)求证:AD⊥PC;
(Ⅱ)当三棱锥B﹣EFC的体积等于四棱锥P﹣ABCD体积的 ![]() 时,求
时,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=9,cosB= ![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A,E之间的距离为 .
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A,E之间的距离为 . 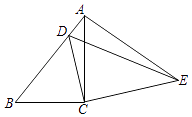
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠ACB=90°,AB=10,sinB= ![]() ,点O是AB的中点,∠DOE=∠A,当∠DOE以点O为旋转中心旋转时,OD交AC的延长线于点D,交边CB于点M,OE交线段BM于点N.
,点O是AB的中点,∠DOE=∠A,当∠DOE以点O为旋转中心旋转时,OD交AC的延长线于点D,交边CB于点M,OE交线段BM于点N.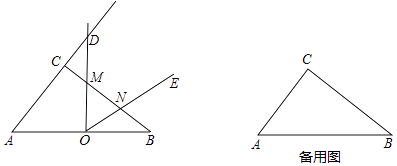
(1)当CM=2时,求线段CD的长;
(2)设CM=x,BN=y,试求y与x之间的函数解析式,并写出定义域;
(3)如果△OMN是以OM为腰的等腰三角形,请直接写出线段CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将笔记本电脑放置在水平桌面上,显示屏OB与底板OA夹角为115°(如图1),侧面示意图为图2;使用时为了散热,在底板下面垫入散热架O′AC后,电脑转到AO′B′的位置(如图3),侧面示意图为图4,已知OA=0B=20cm,B′O′⊥OA,垂足为C. 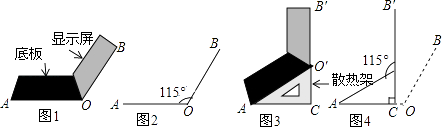
(1)求点O′的高度O′C;(精确到0.1cm)
(2)显示屏的顶部B′比原来升高了多少?(精确到0.1cm)
(3)如图4,要使显示屏O′B′与原来的位置OB平行,显示屏O′B′应绕点O′按顺时针方向旋转多少度? 参考数据:(sin65°=0.906,cos65°=0.423,tan65°=2.146.cot65°=0.446)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE= ![]() AD,过点A作AF∥BC,交EC的延长线于点F.
AD,过点A作AF∥BC,交EC的延长线于点F. 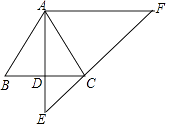
(1)设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,用
,用 ![]() 、
、 ![]() 的线性组合表示
的线性组合表示 ![]() ;
;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
A.△AFD≌△DCE
B.AF= ![]() AD
AD
C.AB=AF
D.BE=AD﹣DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com