
 ,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止.
,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止. cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?
cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?
 解:(1)作AM⊥BC,∵AB=5,sin∠ABC=3/5,
解:(1)作AM⊥BC,∵AB=5,sin∠ABC=3/5, BM=2,
BM=2, BM=2
BM=2 )=10(s)
)=10(s)
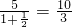
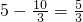
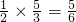 ,
,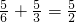 <6
<6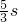 .(不交待理由扣1分)
.(不交待理由扣1分)
 =
= ,
,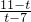 =
= ,
,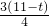 ,
,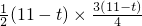 ,
, (t-11)2+18(7<t<11)
(t-11)2+18(7<t<11) (t-11)2+18(7<t<15且t≠11)
(t-11)2+18(7<t<15且t≠11) (t-11)2+18,
(t-11)2+18,

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
| 3 |
| 5 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版) 题型:解答题
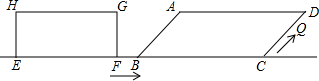
 ,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止.
,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止. cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?
cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?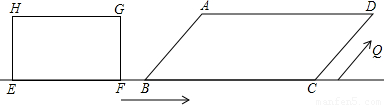
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《四边形》(06)(解析版) 题型:解答题
 ,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止.
,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止. cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?
cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?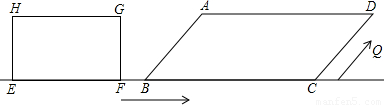
查看答案和解析>>
科目:初中数学 来源:2009年河北省承德市中考数学一模试卷(解析版) 题型:解答题
 ,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止.
,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止. cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?
cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?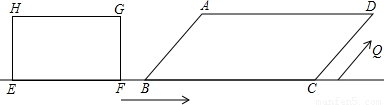
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com