
 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.分析 (1)由AD∥BC得∠1=∠2,所以∠2=∠BEF=50°,从而得∠3=180-∠2-∠BEF;
(2)首先根据边角之间的关系得到BE=BF,结合∠A=∠C′,AB=BC′,证明出△ABE≌△C′BF,进一步得到AE=FC,在Rt△ABE中,利用AB2+AE2=BE2,求出AE的长,进而求出CF的长,即可得到结论.
解答 解:(1)∵AD∥BC,
∴∠1=∠2=50°.
∵∠BEF=∠2=50°,
∴∠3=180-∠2-∠BEF=80°;AD=8,AB=4,
(2)∵∠1=∠2,∠BEF=∠2,
∴∠1=∠BEF,
∴BE=BF,
又∵∠A=∠C′,AB=BC′,
在△ABE与△C′BF中,
$\left\{\begin{array}{l}{BE=BF}\\{∠A=∠C′}\\{AB=BC′}\end{array}\right.$,
∴△ABE≌△C′BF(SAS),
∴AE=C′F.
∵FC=FC′,
∴AE=FC.
在Rt△ABE中,AB2+AE2=BE2.
∵AB=4,AD=8,
∴42+AE2=(8-AE)2,
∴AE=3,
∴CF=AE=3,
∴BF=BC-CF=5.
点评 此题考查图形的翻折变换,全等三角形的判定和性质,勾股定理,解题过程中应注意折叠前后的对应关系,此题难度不大.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条直线相交,组成的图形叫角 | |
| B. | 两条有公共端点的线段组成的图形叫角 | |
| C. | 两条有公共点的射线组成的图形叫角 | |
| D. | 从同一点引出的两条射线组成的图形也是角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,Rt△OAB中,BA⊥OA,且OA=BA=4,点P从O点出发,沿OA以每秒1个单位的速度向A点移动,到达A点停止运动,则△OBP面积S与点P的运动时间t之间的函数图象大致是( )
如图,Rt△OAB中,BA⊥OA,且OA=BA=4,点P从O点出发,沿OA以每秒1个单位的速度向A点移动,到达A点停止运动,则△OBP面积S与点P的运动时间t之间的函数图象大致是( )| A. |  | B. | 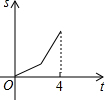 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-2)(m2-m) | B. | m(a-2)(m-1) | C. | m(a-2)(m+1) | D. | m(2-a)(m-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 日期 | 12月22日 | 12月23日 | 12月24日 | 12月25日 |
| 最高气温 | 8℃ | 7℃ | 5℃ | 6℃ |
| 最低气温 | -3℃ | -5℃ | -4℃ | -2℃ |
| A. | 12月22日 | B. | 12月23日 | C. | 12月24日 | D. | 12月25日 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com