Question

如图，AB是⊙O的直径，C是AB延长线上一点，点D在⊙O上，且∠A=30°，∠ABD=2∠BDC ．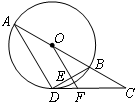

（1）求证：CD是⊙O的切线；
（2）过点O作OF∥AD，分别交BD、CD于点E、F．若OB =2，求 OE和CF的长．

Answer 1

（1）连结OD，根据圆周角定理可得∠ADB=90°，即可求得∠ABD=60°，从而可以求得∠BDC=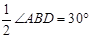，即可证得△ODB是等边三角形，则可得∠ODC=90°，问题得证；（2），

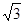解析试题分析：（1）连结OD，根据圆周角定理可得∠ADB=90°，即可求得∠ABD=60°，从而可以求得∠BDC=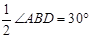，即可证得△ODB是等边三角形，则可得∠ODC=90°，问题得证；
（2）根据平行线的性质可得∠OED=90°，根据垂径定理可得，根据勾股定理可求得OE的长，然后根据∠DOC、∠DOF的正切函数即可求得CD、DF的长，从而可以求得结果.
（1）连结OD

∵AB是⊙O的直径，
∴∠ADB=90°．
∵∠A=30°，
∴∠ABD=60°．
∵∠ABD=2∠BDC，
∴∠BDC=．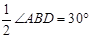
∵OD=OB，
∴△ODB是等边三角形．
∴∠ODB=60°．
∴∠ODC=∠ODB+∠BDC=90°．
∴CD是⊙O的切线；
（2）∵OF∥AD，∠ADB=90°，
∴∠OED=90°
∵BD=OB=2，
∴．
∴．
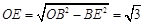∵OD=OB=2，∠DOC=60°，∠DOF=30°，
∴，．
∴．
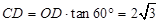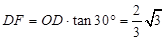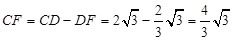考点：圆周角定理，等边三角形的判定和性质，切线的判定，平行线的性质，垂径定理，勾股定理，锐角三角函数的定义
点评：此类问题知识点较多，综合性较强，在中考中比较常见，一般难度不大，需熟练掌握.