
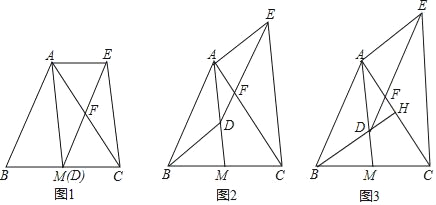
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
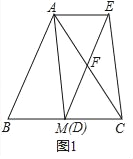
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
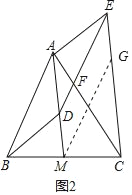
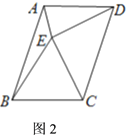
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
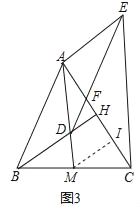
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM.
①求∠CAM的度数;
②当FH=![]() ,DM=4时,求DH的长.
,DM=4时,求DH的长.
【答案】(1)证明见解析;(2)结论:成立.理由见解析;(3)①30°,②1+![]() .
.
【解析】
(1)只要证明AB=ED,AB∥ED即可解决问题;(2)成立.如图2中,过点M作MG∥DE交CE于G.由四边形DMGE是平行四边形,推出ED=GM,且ED∥GM,由(1)可知AB=GM,AB∥GM,可知AB∥DE,AB=DE,即可推出四边形ABDE是平行四边形;
(3)①如图3中,取线段HC的中点I,连接MI,只要证明MI=![]() AM,MI⊥AC,即可解决问题;②设DH=x,则AH=
AM,MI⊥AC,即可解决问题;②设DH=x,则AH=![]() x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出
x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出![]() ,可得
,可得![]() ,解方程即可;
,解方程即可;
(1)证明:如图1中,
∵DE∥AB,
∴∠EDC=∠ABM,
∵CE∥AM,
∴∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,
∴BD=DC,
∴△ABD≌△EDC,
∴AB=ED,∵AB∥ED,
∴四边形ABDE是平行四边形.
(2)结论:成立.理由如下:
如图2中,过点M作MG∥DE交CE于G.
∵CE∥AM,
∴四边形DMGE是平行四边形,
∴ED=GM,且ED∥GM,
由(1)可知AB=GM,AB∥GM,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
(3)①如图3中,取线段HC的中点I,连接MI,
∵BM=MC,
∴MI是△BHC的中位线,
∴MI∥BH,MI=![]() BH,
BH,
∵BH⊥AC,且BH=AM.
∴MI=![]() AM,MI⊥AC,
AM,MI⊥AC,
∴∠CAM=30°.
②设DH=x,则AH=![]() x,AD=2x,
x,AD=2x,
∴AM=4+2x,
∴BH=4+2x,
∵四边形ABDE是平行四边形,
∴DF∥AB,
∴![]() ,
,
∴![]() ,
,
解得x=1+![]() 或1﹣
或1﹣![]() (舍弃),
(舍弃),
∴DH=1+![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
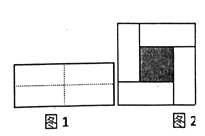
【题目】把一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1).
的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1).
(1)请用两种不同的方法求图2中阴影部分的面积(直接用含![]() ,
,![]() 的代数式表示)
的代数式表示)
方法1:________,方法2:____;
(2)根据(1)中结论,请你写出下列三个代数式![]() ,
,![]() ,
,![]() 间的等量关系:____;
间的等量关系:____;
(3)根据(2)题中的等量关系,解决如下问题:己知实数![]() 、
、![]() 满足
满足![]() ,
,![]() ,请求出
,请求出![]() 的值:
的值:
(4)已知![]() ,请求出
,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
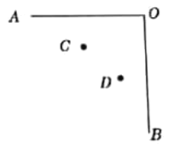
【题目】某中学八(2)班举行文艺晚会,桌子摆成如图所示两直排(图中的![]() ,
,![]() ),
),![]() 桌面上摆满了橘子,
桌面上摆满了橘子,![]() 桌面上摆满了糖果,站在
桌面上摆满了糖果,站在![]() 处的学生小明先拿橘子再拿糖果,然后到
处的学生小明先拿橘子再拿糖果,然后到![]() 处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短.(要求:简略叙述作图过程,实走路线用实线,其它辅助线用虚线)
处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短.(要求:简略叙述作图过程,实走路线用实线,其它辅助线用虚线)
查看答案和解析>>
科目:初中数学 来源: 题型:
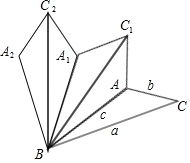
【题目】在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为_____________.(结果用含有a,b,c的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
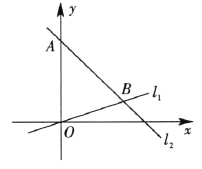
【题目】如图,在平面直角坐标系内,点![]() 的坐标为(0,24),经过原点的直线
的坐标为(0,24),经过原点的直线![]() 与经过点
与经过点![]() 的直线
的直线![]() 相交于点
相交于点![]() ,点
,点![]() 的坐标为(18,6).
的坐标为(18,6).
(1)求直线![]() ,
,![]() 对应的函数表达式;
对应的函数表达式;
(2)点![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),作
重合),作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设点
,设点![]() 的纵坐标为
的纵坐标为![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() ,则
,则![]() ___
___![]() .
.
(2)若把(1)中![]() 改为
改为![]() ,其它条件不变,请用含
,其它条件不变,请用含![]() 的式子表示
的式子表示![]() ,并证明 你的结论.
,并证明 你的结论.
(3)如图2,四边形![]() 中,
中,![]() ,点
,点![]() 在四边形
在四边形![]() 内部,在
内部,在![]() 中,
中,![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
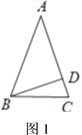
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一段![]() 米长的河堤的整治任务,打算请
米长的河堤的整治任务,打算请![]() 两个工程队来完成,经过调查发现,
两个工程队来完成,经过调查发现,![]() 工程队每天比
工程队每天比![]() 工程队每天多整治
工程队每天多整治![]() 米,
米,![]() 工程队单独整治的工期是
工程队单独整治的工期是![]() 工程队单独整治的工期的
工程队单独整治的工期的![]() .
.
(1)问![]() 工程队每天分别整治多少米?
工程队每天分别整治多少米?
(2)由![]() 两个工程队先后接力完成,共用时
两个工程队先后接力完成,共用时![]() 天,问
天,问![]() 工程队分别整治多少米?
工程队分别整治多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com