
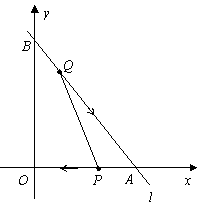
如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,且
,且![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,动点
两点,动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒2个单位长度的速度向点
上以每秒2个单位长度的速度向点![]() 移动,同时动点
移动,同时动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 移动,设点P、Q移动的时间为
移动,设点P、Q移动的时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() 是以PQ为底的等腰三角形?
是以PQ为底的等腰三角形?
(2)求出点P、Q的坐标;(用含![]() 的式子表达)
的式子表达)
(3)当![]() 为何值时,
为何值时,![]() 的面积是△ABO面积的
的面积是△ABO面积的![]() ?
?
解:
解: (1)当AQ=AP时,是以PQ为底的等腰三角形.
由解析式可得A(6,0),B(0,8) (1分)
由勾股定理得,AB=10
∴AQ=10-2t,AP=t
即10-2t=t
 ∴
∴![]() (秒)…………(3分)
(秒)…………(3分)
当![]() 时,是以PQ为底的等腰三角形。…………(4分)
时,是以PQ为底的等腰三角形。…………(4分)
(2)过Q点分别向x轴,y轴引垂线,垂足分别是M,N.
设Q(x,y)
由题意可知BQ=2t,AP=t
△BQN∽△QMA∽△BOA
∴![]()
![]() ∴
∴![]()
![]()
∴![]() ,
, ![]()
![]() 的坐标分别是
的坐标分别是![]() ,(6-t,0)…(7分)
,(6-t,0)…(7分)
(3)∵![]() 的面积=
的面积=![]() . △AOB的面积=
. △AOB的面积=![]()
∴![]()
解得,t1=2,t2=3
当t1=2秒或,t2=3秒时,![]() 的面积是△ABO面积的
的面积是△ABO面积的![]() .…………(11分)
.…………(11分)


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
 (2010•资阳)如图,已知直线l:y=kx+b与双曲线C:y=
(2010•资阳)如图,已知直线l:y=kx+b与双曲线C:y=| m |
| x |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知直线l:y=-2x+12交x轴于点A,交y轴于点B,点C在线段OB上运动(不与O、B重合),连接AC,作CD⊥AC,交线段AB于点D.
如图,已知直线l:y=-2x+12交x轴于点A,交y轴于点B,点C在线段OB上运动(不与O、B重合),连接AC,作CD⊥AC,交线段AB于点D.查看答案和解析>>
科目:初中数学 来源:黑龙江省期中题 题型:解答题
如图,已知直线的函数表达式为 ,且l与x轴,y轴分别交于A,B两点,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点P、Q移动的时间为t秒。
,且l与x轴,y轴分别交于A,B两点,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点P、Q移动的时间为t秒。

 ?
?查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,且
,且![]() 与x轴,y轴分别交于
与x轴,y轴分别交于![]() 两点,动点
两点,动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒2个单位长度的速度向点
上以每秒2个单位长度的速度向点![]() 移动,同时动点
移动,同时动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 移动,设点
移动,设点![]() 移动的时间为t秒.(1)求出点
移动的时间为t秒.(1)求出点![]() 的坐标;(2)当t为何值时,
的坐标;(2)当t为何值时,![]() 与
与![]() 相似?(3)求出(2)中当
相似?(3)求出(2)中当![]() 与
与![]() 相似时,线段
相似时,线段![]() 所在直线的函数表达式.
所在直线的函数表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com