
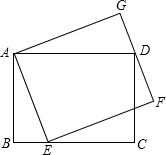
 (2013•宁德质检)如图,已知矩形ABCD,动点E从点B沿线段BC向点C运动,连结AE、DE,以AE为边作矩形AG,使边FG过点D.
(2013•宁德质检)如图,已知矩形ABCD,动点E从点B沿线段BC向点C运动,连结AE、DE,以AE为边作矩形AG,使边FG过点D.| 3 |
| AB |
| AG |
| AE |
| AD |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 6 |
| 6 |
| 6 |
| 120π×3 |
| 180 |


科目:初中数学 来源: 题型:
 (2013•宁德质检)一个材质均匀的正方体六个面上分别标有文字”祝、你、天、天、快、乐”掷这个正方体,结果的其表面展开图如图所示,随机抛“天”字朝上的概率是( )
(2013•宁德质检)一个材质均匀的正方体六个面上分别标有文字”祝、你、天、天、快、乐”掷这个正方体,结果的其表面展开图如图所示,随机抛“天”字朝上的概率是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 按一定的规律组成,其中第1个图形有2个,第 2个图形中有6个,第3个图形中有12个…,则第30个图形中
按一定的规律组成,其中第1个图形有2个,第 2个图形中有6个,第3个图形中有12个…,则第30个图形中 的个数是( )
的个数是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com