证明:(1)∵AF=AC,AD=AB,∠DAC=∠BAC+∠DAB,∠BAF=∠BAC+∠CAF,
而∠DAB=∠CAF=60°
∴∠DAC=∠BAF,
∴△ABF≌△ADC(SAS);
(2)∵∠ACB=∠CAF=60°,
∴AF∥BC,平行线间垂线段处处相等
∵△ABF与△ACF是同底AF等高的,
∴S
△ABF=S
△ACF;
(3)判定:S
四边形ACBD=S
△BCE+S
△ACF.
作DM⊥BC交BC延长线于点M,作BN⊥EC交EC于点N,
∵△ABF≌△ADC,∴CD=BF,∠1=∠2,∠1+∠3=∠2+∠4=60°,
∴∠3=∠4,而∠DMC=∠BNF=90°,
∴△DMC≌△BNF,∴DM=BN,
∵△BCD与△BCE的底EC、BC相等,高DM=BN,
∴S
△BCD=S
△BCE∴S
四边形ACBD=S
△BCE+S
△ACF.
分析:(1)根据角相互间的等量关系得出∠DAC=∠BAF,通过SAS即可证明△ABF≌△ADC;
(2)根据平行线的判定和性质结合图形可以得出△ABF与△ACF是同为底AF,高是等高的,根据三角形的面积公式即可得出S
△ABF=S
△ACF;
(3)由图知:S
四边形ACBD=S
△ACD+S
△BCD,而△ABF≌△ADC,∴S
△ACD=S
△ABF=S
△ACF,∴只需证明S
△BCD=S
△BCE即可.
点评:本题考查了全等三角形的判定与性质和三角形的面积计算,等底(同底)等高的三角形面积相等.

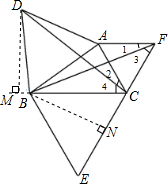
 如图所示,已知△ABC中,∠ACB=60°,分别以AB、BC、CA为边向外作等边三角形ABD、等边三角形BCE、等边三角形ACF;用“S”表示面积.
如图所示,已知△ABC中,∠ACB=60°,分别以AB、BC、CA为边向外作等边三角形ABD、等边三角形BCE、等边三角形ACF;用“S”表示面积. 证明:(1)∵AF=AC,AD=AB,∠DAC=∠BAC+∠DAB,∠BAF=∠BAC+∠CAF,
证明:(1)∵AF=AC,AD=AB,∠DAC=∠BAC+∠DAB,∠BAF=∠BAC+∠CAF,

 习题精选系列答案
习题精选系列答案