
 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
 (2012•成华区一模)已知两直线l1、l2分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.
(2012•成华区一模)已知两直线l1、l2分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.| 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| M(l) |
| M(l) |
| M(m) |
| M(m) |
查看答案和解析>>
科目:初中数学 来源:2008年江苏省南京市建邺区中考数学一模试卷(解析版) 题型:解答题
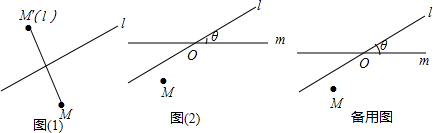
 ,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换 ,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换 ,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为 ,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题: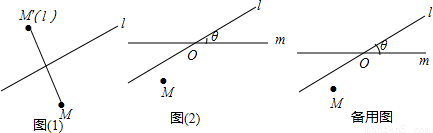
查看答案和解析>>
科目:初中数学 来源:2009年江苏省南京市中考数学模拟卷(解析版) 题型:解答题
 ,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换 ,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换 ,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为 ,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题: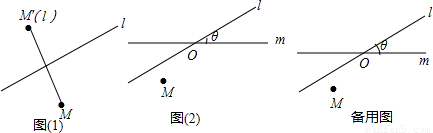
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com