
��ͼ1��������y=ax2+bx+c��a��0���Ķ���ΪM��ֱ��y=m��x��ƽ�У����������߽��ڵ�A��B������AMBΪ����ֱ�������Σ����ǰ���������A��B����֮��IJ������߶�ABΧ�ɵ�ͼ�γ�Ϊ�������߶�Ӧ�����Σ��߶�AB��Ϊ����������M��Ϊ��������M���߶�AB�ľ����Ϊ���ߣ�
��1��������y= x2��Ӧ�ĵ���Ϊ�� ����������y=4x2��Ӧ�ĵ���Ϊ�� ����������y=ax2��a��0����Ӧ�ĵ���Ϊ������������y=a��x��2��2+3��a��0����Ӧ�ĵ���Ϊ������
x2��Ӧ�ĵ���Ϊ�� ����������y=4x2��Ӧ�ĵ���Ϊ�� ����������y=ax2��a��0����Ӧ�ĵ���Ϊ������������y=a��x��2��2+3��a��0����Ӧ�ĵ���Ϊ������
��2��������y=ax2��4ax�� ��a��0����Ӧ�ĵ���Ϊ6������x���ϣ���a��ֵ��
��a��0����Ӧ�ĵ���Ϊ6������x���ϣ���a��ֵ��
��3����������y=anx2+bnx+cn��an��0���Ķ�Ӧ���μ�ΪFn��n=1��2��3����������F1��F2������FnΪ�������Σ���Ӧ�ĵ���֮�ȼ�Ϊ���Ʊȣ���Fn��Fn��1�����Ʊ�Ϊ ����Fn�ĵ�����Fn��1�ĵ������е㣬�ֽ���2������õ�������Ϊy1�����Ӧ�����μ�ΪF1��
����Fn�ĵ�����Fn��1�ĵ������е㣬�ֽ���2������õ�������Ϊy1�����Ӧ�����μ�ΪF1��
����������y2�ı���ʽ��
����F1�ĵ���Ϊh1��F2�ĵ���Ϊh2����Fn�ĵ���Ϊhn����hn=������Fn�ĵ����ж˵������Ϊ��2����F1��F2������Fn�ĵ����Ҷ˵��Ƿ���һ��ֱ���ϣ����ǣ�ֱ��д����ֱ�ߵı���ʽ�������ǣ���˵�����ɣ�
��1��4��1�� ��
�� ��
��
���������������1�����ݶ�������y=ax2��a��0���ĵ���Ϊ ������Ϊ
������Ϊ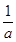 ������������
������������ ��ͨ��ƽ��y=ax2��a��0���õ����õ�����Ϊ
��ͨ��ƽ��y=ax2��a��0���õ����õ�����Ϊ ������Ϊ
������Ϊ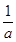 ���ɴ˿ɵõ���������ֻ��a�йأ������أ��Ӷ��ɵã�
���ɴ˿ɵõ���������ֻ��a�йأ������أ��Ӷ��ɵã�
��2���ɣ�1���Ľ��ۣ����ݵ�����a��ֵ��
��3���ٸ���y1�����õ�y2��
�ڽ�ϻ�ͼ����֪h1��h2��h3������hn��1��hn����ֱ��x=2�ϣ����Կ���hn��hn��1���Ҷ���Fn��1�ĵ����е㣬�����ɵã���ͼʱ��֪�����й��ɵݼ����ɴ˿ɵ��Ҷ˵���ص㣮���ڡ�F1��F2������Fn�ĵ����Ҷ˵��Ƿ���һ��ֱ���ϣ��������ǿ����Ʋ��������ڵ������Ƿ���һ��ֱ���ϣ�������ڵ������㲻��������۲���������֮����������Կ��Կ��ǻ����ļ���ͼ�ι�ϵ�������������ֱ�߷��̼��ɣ�
�����������1��4��1�� ��
�� ��
��
��a��0��
��y=ax2��ͼ��������£�
��ع�ԭ��O����ABΪ�������AB��y��Ľ���ΪC������OA��OB��
�ߡ�DABΪ����ֱ�������Σ�AB��x�ᣬ
��OC��AB��
���OCA=��OCB= ��AOB=
��AOB= ��90��=45�㣬
��90��=45�㣬
���ACO���BCO��Ϊ����ֱ�������Σ�
��AC=OC=BC��
��xA=-yA��xB=yB������y=ax2��
��A����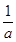 ��
��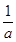 ����B��
����B��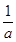 ��
��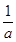 ����C��0��
����C��0��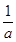 ����
����
��AB= ��OC=
��OC=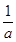 ��
��
��y=ax2�ĵ���Ϊ ��
��
��������y= x2��Ӧ��a=
x2��Ӧ��a= ���õ���
���õ��� Ϊ4��
Ϊ4��
��������y=4x2��Ӧ��a=4���õ���Ϊ Ϊ
Ϊ ��
��
��������y=ax2��a��0��������Ϊ ��
��
��������y=a��x��2��2+3��a��0���ɿ���y=ax2����ƽ��2����λ���ȣ�������ƽ��3����λ���Ⱥ�õ���ͼ�Σ�
��ƽ�Ʋ��ı���״����С������
��������y=a��x��2��2+3��a��0����������������y=ax2������ȫ�ȣ�
��������y=ax2��a��0��������Ϊ ��
��
��������y=a��x��2��2+3��a��0��������Ϊ ��
��
��2����y=ax2��4ax�� ��
��
���ɣ�1���������Ϊ ��
��
��y=ax2��4ax�� �ĵ���Ϊ6��
�ĵ���Ϊ6��
�� =6��
=6��
���A= ��
��
��y= x2��
x2�� x��
x�� =
= ��x��2��2��3
��x��2��2��3
��3���١�F1�ĵ�����F2�ĵ���=2��1��
�� =
= ��
��
��a1= ��
��
��a2= ��
��
��y= ��x��2��2��3�ĵ���AB��x���ϣ�A��B��ߣ���
��x��2��2��3�ĵ���AB��x���ϣ�A��B��ߣ���
��A����1��0����B��5��0����
��F2�ĵ�������Ϊ��2��0����
��y2= ��x��2��2��
��x��2��2��
�ڡ�Fn������Ϊ����ֱ�������Σ�
��Fn�ĵ���Ϊ2hn��
��2hn��2hn��1=1��2��
��hn= hn��1=��
hn��1=�� ��2hn��2=��
��2hn��2=�� ��3hn��3=��=��
��3hn��3=��=�� ��n+1h1��
��n+1h1��
��h1=3��
��hn=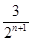 ��
��
��hn��hn��1���Ҷ���Fn��1�ĵ����е㣬
��h1��h2��h3������hn��1��hn����һ��ֱ���ϣ�
��h1��ֱ��x=2�ϣ�
��h1��h2��h3������hn��1��hn����ֱ��x=2�ϣ�
��Fn�ĵ����Ҷ˵������Ϊ2+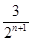 ��
��
����F1��F2������Fn�ĵ����Ҷ˵���һ��ֱ���ϣ�ֱ��Ϊy=��x+5��
�������£�
����Fn��2��Fn��1��Fn���Σ���ϵ��ͼ2��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�������
ijˮ������������ÿ�����Ϊ40Ԫ��ƻ������۲��Ź涨ÿ���ۼ۲��ø���55Ԫ���г����鷢�֣���ÿ����50Ԫ�ļ۸����ۣ�ƽ��ÿ������90�䣬�۸�ÿ���1Ԫ��ƽ��ÿ��������3�䣮
��1����ƽ��ÿ�������� �������ۼ�
�������ۼ� Ԫ/��֮��ĺ�����ϵʽ��
Ԫ/��֮��ĺ�����ϵʽ��
��2�����������ƽ��ÿ�����������w��Ԫ�������ۼ� ��Ԫ/�䣩֮��ĺ�����ϵʽ��
��Ԫ/�䣩֮��ĺ�����ϵʽ��
��3����ÿ��ƻ�������ۼ�Ϊ����Ԫʱ�����Ի�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��� ��
�� ��
�� ��������
�������� �ֱ��ڱ�
�ֱ��ڱ� �ϻ�������
�ϻ������� ����
���� ��������������
Ϊ��������������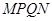 ������߳�Ϊ
������߳�Ϊ ��������
��������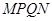 ��
�� �������ֵ����Ϊ
�������ֵ����Ϊ ��
��
��1�� �б�
�б� �ϸ�
�ϸ� ��
��
��2���� ʱ��
ʱ�� ǡ�����ڱ�
ǡ�����ڱ� �ϣ���ͼ1����
�ϣ���ͼ1����
��3���� ��
�� �ⲿʱ����ͼ2������
�ⲿʱ����ͼ2������ ����
���� �ĺ�����ϵʽ��ע��
�ĺ�����ϵʽ��ע�� ��ȡֵ��Χ���������
��ȡֵ��Χ��������� Ϊ��ֵʱ
Ϊ��ֵʱ ������ֵ�Ƕ��٣�
������ֵ�Ƕ��٣� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��������y=�� x2+
x2+ x��2��x����A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C���ֱ����B��C��y�ᣬx���ƽ���ߣ���ƽ���߽��ڵ�D������BDC�Ƶ�C��ʱ����ת��ʹ��D��ת��y���ϵõ���FEC������BF��
x��2��x����A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C���ֱ����B��C��y�ᣬx���ƽ���ߣ���ƽ���߽��ڵ�D������BDC�Ƶ�C��ʱ����ת��ʹ��D��ת��y���ϵõ���FEC������BF��
��1�����B��C����ֱ�ߵĺ�������ʽ��
��2�����BCF�������
��3�����߶�BC���Ƿ���ڵ�P��ʹ���Ե�P��A��BΪ��������������BOC���ƣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪������ ��x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC��
��x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC��
��1��ֱ��д��A��D��C��������ꣻ
��2������M���������ϣ�ʹ�á�MAD��������CAD�������ȣ����M�����ꣻ
��3�����C���������߶Գ���ĶԳƵ�ΪB�������������Ƿ���ڵ�P��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊ���Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��������y=�� x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A����1��0����C��0��2����
x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A����1��0����C��0��2����
��1���������ߵı���ʽ��
��2���������ߵĶԳ������Ƿ���ڵ�P��ʹ��PCD����CDΪ���ĵ��������Σ�������ڣ�ֱ��д��P������ꣻ��������ڣ���˵�����ɣ�
��3����Eʱ�߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ���ı���CDBF������������ı���CDBF������������ʱE������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ƽ��ֱ������ϵ �У����κ���
�У����κ��� ��
��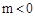 ����ͼ����
����ͼ����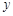 �������ύ��A�㣮
�������ύ��A�㣮
��1����֤���ö��κ�����ͼ����x������������㣻
��2����ö��κ�����ͼ����x��������������Ҳ�Ľ���Ϊ��B������ABO=45�㣬��ֱ��AB����ƽ��2����λ�õ�ֱ��l����ֱ��l�Ľ���ʽ��
��3���ڣ�2���������£���M��p��q��Ϊ���κ���ͼ���ϵ�һ�����㣬�� ʱ����M����x��ĶԳƵ㶼��ֱ��l���·�����m��ȡֵ��Χ��
ʱ����M����x��ĶԳƵ㶼��ֱ��l���·�����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�������� ����A
����A ��C��0��4�����㣬��x�����һ������B��
��C��0��4�����㣬��x�����һ������B��
��1���������ߵĽ���ʽ��
��2������ �ڵ�һ�����������ϣ����D����ֱ��BC�ĶԳƵ�
�ڵ�һ�����������ϣ����D����ֱ��BC�ĶԳƵ� �����ꣻ
�����ꣻ
��3���ڣ�2���������£�����D��DE��BC�ڵ�E,���������� ��ͼ����E����
��ͼ����E���� �ڴ˷���������ͼ���ϣ���
�ڴ˷���������ͼ���ϣ��� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB = ��EDF = 90�㣬��DEF = 45�㣬AC =" 8" cm��BC =" 6" cm��EF =" 9" cm��
��ͼ��2������DEF��ͼ��1����λ�ó�������1 cm/s���ٶ���CB���ABC�����ƶ����ڡ�DEF�ƶ���ͬʱ����P�ӡ�ABC�Ķ���B��������2 cm/s���ٶ���BA���A�����ƶ�������DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ�ƶ�����PҲ��ֹ֮ͣ�ơ�DE��AC�ཻ�ڵ�Q������PQ�����ƶ�ʱ��Ϊt��s����0��t��4.5��������������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE�����ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɡ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɡ���ͼ��3����ͬѧ������ʹ�ã�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com