
【题目】某塑料厂生产一种家用塑料制品,它的成本是![]() 元
元![]() 件,售价是
件,售价是![]() 元
元![]() 件,年销售量为
件,年销售量为![]() 万件.为了获得更好的效益,厂家准备拿出一定的资金做广告.根据测算,若每年投入广告费
万件.为了获得更好的效益,厂家准备拿出一定的资金做广告.根据测算,若每年投入广告费![]() 万元,产品的年销售量将是原销售量的
万元,产品的年销售量将是原销售量的![]() 倍,且
倍,且![]() 与
与![]() 之间满足
之间满足![]() ,具体数量如下表:
,具体数量如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润![]() (万元)与广告费用
(万元)与广告费用![]() (万元)的函数关系式,并计算每年投入的广告费是多少万元时,所获得的利润最大?
(万元)的函数关系式,并计算每年投入的广告费是多少万元时,所获得的利润最大?
(3)如果厂家希望年利润![]() (万元)不低于
(万元)不低于![]() 万元,请你帮助厂家确定广告费
万元,请你帮助厂家确定广告费![]() 的范围.
的范围.
【答案】(1)![]() ;(2)年利润
;(2)年利润![]() (万元)与广告费用
(万元)与广告费用![]() (万元)的函数关系式为
(万元)的函数关系式为![]() ,每年投入的广告费是
,每年投入的广告费是![]() 万元时,所获得的利润最大,为
万元时,所获得的利润最大,为![]() 万元;(3)当
万元;(3)当![]() 时,年利润
时,年利润![]() (万元)不低于
(万元)不低于![]() 万元.
万元.
【解析】
(1)根据y与x的函数关系式为y=ax2+bx+1,由待定系数法求出a,b即可;
(2)由“利润=销售总额-成本费用-广告费用”可以表示出W与x之间的关系式;
(3)当y=14时代入(2)的解析式求出x的值,由二次函数的图象特征就可以得出结论.
解:(1)由题意将(1,1.5),(2,1.8)代入![]() ,得
,得
![]() ,解得
,解得![]() ,
,
![]() ;
;
(2)由题意,得![]() ,
,
![]() ,
,![]() 当
当![]() 时,
时,![]() .
.
答:年利润![]() (万元)与广告费用
(万元)与广告费用![]() (万元)的函数关系式为
(万元)的函数关系式为![]() ,每年投入的广告费是
,每年投入的广告费是![]() 万元时,所获得的利润最大,最大利润为
万元时,所获得的利润最大,最大利润为![]() 万元;
万元;
(3)当![]() 时,
时,![]() ,
,
解得![]() ,
,![]() ,
,
![]() 当
当![]() 时,年利润
时,年利润![]() (万元)不低于
(万元)不低于![]() 万元.
万元.


科目:初中数学 来源: 题型:
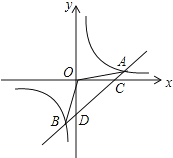
【题目】如图,一次函数y=x+b和反比例函数y=![]() (k≠0)交于点A(4,1).
(k≠0)交于点A(4,1).
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了奖励优秀班集体,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3幅乒乓球拍和2幅羽毛球拍共需204元.
(1)每副乒乓球拍和羽毛球拍的单价各是多少元?
(2)若学校购买5副乒乓球拍和3副羽毛球拍,一共应支出多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
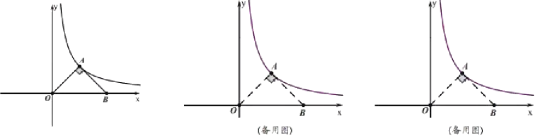
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为原点
为原点![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系,
轴建立平面直角坐标系,![]() 的顶点
的顶点![]() 在反比例函数
在反比例函数![]() 的图象上.
的图象上.
(1)求反比例函数的解析式:
(2)将![]() 向右平移
向右平移![]() 个单位长度,对应得到
个单位长度,对应得到![]() ,当函数
,当函数![]() 的图象经过
的图象经过![]() 一边的中点时,求
一边的中点时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于点A、B,与y轴分别交于点C,其中点
与x轴交于点A、B,与y轴分别交于点C,其中点![]() ,点
,点![]() ,且
,且![]() .
.
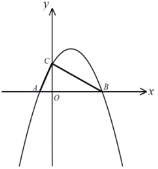
(1)求抛物线的解析式;
(2)点P是线段AB上一动点,过P作![]() 交BC于D,当
交BC于D,当![]() 面积最大时,求点P的坐标;
面积最大时,求点P的坐标;
(3)点M是位于线段BC上方的抛物线上一点,当![]() 恰好等于
恰好等于![]() 中的某个角时,求点M的坐标.
中的某个角时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
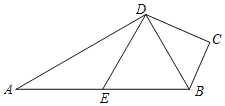
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC=![]() ,求EC的长.
,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
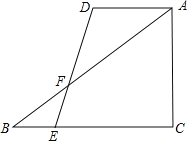
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,AD∥BC,DE与AB交于点F,已知AD=4,DF=2EF,sin∠DAB=![]() ,则线段DE=_____.
,则线段DE=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com