
ЁОЬтФПЁПШчЭМ1ЫљЪОЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌгыХзЮяЯпСэвЛИіНЛЕуЮЊ
ЃЌгыХзЮяЯпСэвЛИіНЛЕуЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§
ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§![]() Еузї
Еузї![]() жсгкЕу
жсгкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]()
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪН
ЃЈ2ЃЉЕБЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЗНЃЌЧв
ЩЯЗНЃЌЧв![]() ЪЧвд
ЪЧвд![]() ЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌЧѓ
ЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌЧѓ![]() ЕФзјБъ
ЕФзјБъ
ЃЈ3ЃЉШчЭМ2ЫљЪОЃЌШєЕу![]() ЮЊЖдГЦжсгвВрХзЮяЯпЩЯвЛЕуЃЌСЌНг
ЮЊЖдГЦжсгвВрХзЮяЯпЩЯвЛЕуЃЌСЌНг![]() ЃЌвд
ЃЌвд![]() ЮЊжБНЧЖЅЕуЃЌЯпЖЮ
ЮЊжБНЧЖЅЕуЃЌЯпЖЮ![]() ЮЊНЯГЄжБНЧБпЃЌЙЙдьСНжБНЧБпБШЮЊ
ЮЊНЯГЄжБНЧБпЃЌЙЙдьСНжБНЧБпБШЮЊ![]() ЕФ
ЕФ![]() ЃЌЪЧЗёДцдкЕу
ЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() ЧЁКУТфдкжБЯп
ЧЁКУТфдкжБЯп![]() ЩЯЃПШєДцдкЃЌЧыжБНгаДГіЯргІЕу
ЩЯЃПШєДцдкЃЌЧыжБНгаДГіЯргІЕу![]() ЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
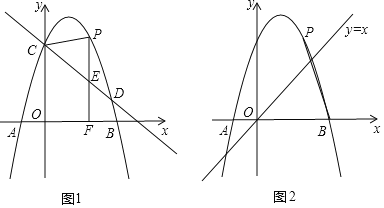
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉP
ЃЛЃЈ2ЃЉP ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉДцдкЃЌ2Лђ
ЃЛЃЈ3ЃЉДцдкЃЌ2Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЯШАбCЕуДњШыжБЯпCDжаЧѓГіmЕФжЕЃЌБэЪОP(mЃЌ-m2+2m+3)ЁЂE(mЃЌ![]() m+3)ЃЌЕБЁїCPEЪЧвдCEЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌШЛКѓЗжЗжСНжжЧщПіЃКЂйЕБCE=CPЪБЃЌЂкЕБCE=PEЪБЃЛ
m+3)ЃЌЕБЁїCPEЪЧвдCEЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌШЛКѓЗжЗжСНжжЧщПіЃКЂйЕБCE=CPЪБЃЌЂкЕБCE=PEЪБЃЛ
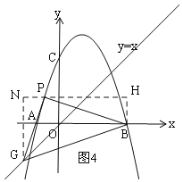
ЃЈ3ЃЉЯШИљОнЕуPдкХзЮяЯпЩЯЃЌGдкжБЯпy=xЩЯЩшP(mЃЌ-m2+2m+3)ЃЌG(aЃЌa)ЃЌ
ШчЭМ3ЃЌзїИЈжњЯпЃЌЙЙНЈСНИіЯрЫЦШ§НЧаЮЃЌжЄУїЁїPHGЁзЁїBNPЃЌдђ![]() ЃЌгЩСНжБНЧБпБШЮЊ1ЃК2СаЗНГЬзщНтГіКсзјБъmЃЛШчЭМ4ЃЌЭЌРэСаЗНГЬзщНтГіmЕФжЕЃЎ
ЃЌгЩСНжБНЧБпБШЮЊ1ЃК2СаЗНГЬзщНтГіКсзјБъmЃЛШчЭМ4ЃЌЭЌРэСаЗНГЬзщНтГіmЕФжЕЃЎ
НтЃКЃЈ1ЃЉАбЕу![]() ЕФзјБъДњШыХзЮяЯп
ЕФзјБъДњШыХзЮяЯп![]() жаЃЌ
жаЃЌ
ЕУЃК![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЫљвдХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉАб![]() ДњШы
ДњШы![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
ЫљвджБЯпЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
Щш![]() ЃЌ
ЃЌ
ЂйЕБ![]() ЪБЃЌзї
ЪБЃЌзї![]() ЃЌШчЭМ2ЃЌ
ЃЌШчЭМ2ЃЌ
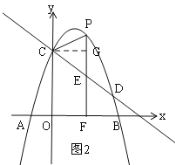
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЙДЙЩЖЈРэЕУ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
НтЕУ![]() (ЩсШЅ)ЃЌ
(ЩсШЅ)ЃЌ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБ
ЪБ![]() ЃЌ
ЃЌ
злЩЯЫљЪіЕБШ§НЧаЮ![]() ЪЧвд
ЪЧвд![]() ЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌЕуPЕФзјБъЮЊ
ЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌЕуPЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕуPЕФКсзјБъЮЊ2Лђ![]() ЃЎ
ЃЎ
ЩшP(mЃЌ-m2+2m+3)ЃЌG(aЃЌa)ЃЌ
ШчЭМ3ЃЌ
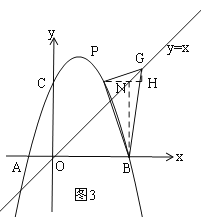
Й§BзїBNЁЮyжсЃЌЙ§PзїPHЁЮxжсЃЌНЛгкNЃЌЙ§GзїGHЁЭPNЃЌДЙзуЮЊHЃЌдђЁЯPHG=ЁЯBNP=90ЁуЃЌ
ЁрЁЯNBP+ЁЯBPN=90ЁуЃЌ
ЁпЁЯBPG=90ЁуЃЌ
ЁрЁЯBPN+ЁЯNPG=90ЁуЃЌ
ЁрЁЯNBP=ЁЯNPGЃЌ
ЁрЁїPHGЁзЁїBNPЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() =2ЃЌ
=2ЃЌ
Ёр![]() =2ЃЌ
=2ЃЌ
Ёр![]() =2ЃЌ
=2ЃЌ
дђ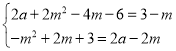 ЃЌ
ЃЌ
НтЕУЃКm1=-3ЃЈЩсШЅЃЉЃЌm2=2ЃЛ
ШчЭМ4ЃЌ
Й§PзїNHЁЮxжсЃЌЙ§GзїGNЁЭNHЃЌЙ§BзїBHЁЭNHЃЌДЙзуЗжБ№ЮЊNЁЂHЃЌ
ЭЌРэЕУЃКЁїPNGЁзЁїBHPЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр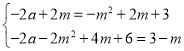 ЃЌ
ЃЌ
НтЕУЃКm1=![]() ЃЈЩсШЅЃЉЃЌm2=
ЃЈЩсШЅЃЉЃЌm2=![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌЯргІЕуPЕФКсзјБъЮЊ2Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
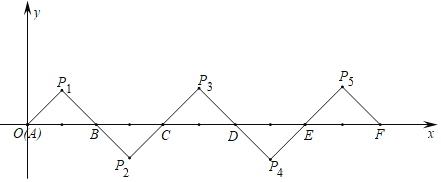
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧЕШбќжБНЧШ§НЧаЮЧв
ЪЧЕШбќжБНЧШ§НЧаЮЧв![]() ЃЌАб
ЃЌАб![]() ШЦЕуBЫГЪБеыа§зЊ
ШЦЕуBЫГЪБеыа§зЊ![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌАб
ЃЌАб![]() ШЦЕуCЫГЪБеыа§зЊ
ШЦЕуCЫГЪБеыа§зЊ![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌвРДЫРрЭЦЃЌЕУЕНЕФЕШбќжБНЧШ§НЧаЮЕФжБНЧЖЅЕу
ЃЌвРДЫРрЭЦЃЌЕУЕНЕФЕШбќжБНЧШ§НЧаЮЕФжБНЧЖЅЕу![]() ЕФзјБъЮЊ__________ЃЎ
ЕФзјБъЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
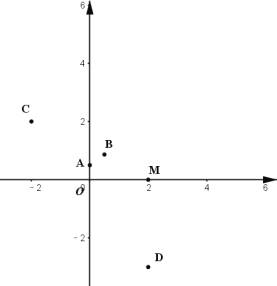
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЖдгкФГЕу
жаЃЌЖдгкФГЕу![]() ЃЈ
ЃЈ![]() ВЛЪЧдЕуЃЉЃЌГЦвдЕу
ВЛЪЧдЕуЃЉЃЌГЦвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ГЄЮЊАыОЖЕФдВЮЊЕу
ГЄЮЊАыОЖЕФдВЮЊЕу![]() ЕФАыГЄдВЃЛЖдгкЕу
ЕФАыГЄдВЃЛЖдгкЕу![]() ЃЌШєНЋЕу
ЃЌШєНЋЕу![]() ЕФАыГЄдВ
ЕФАыГЄдВ![]() ШЦдЕуа§зЊЃЌФмЙЛЪЙЕУЕу
ШЦдЕуа§зЊЃЌФмЙЛЪЙЕУЕу![]() ЮЛгкЕу
ЮЛгкЕу![]() ЕФАыГЄдВФкВПЛђдВЩЯЃЌдђГЦЕу
ЕФАыГЄдВФкВПЛђдВЩЯЃЌдђГЦЕу![]() ФмБЛЕу
ФмБЛЕу![]() АыГЄВЖЛёЃЈЛђЕу
АыГЄВЖЛёЃЈЛђЕу![]() ФмАыГЄВЖЛёЕу
ФмАыГЄВЖЛёЕу![]() ЃЉЃЎ
ЃЉЃЎ
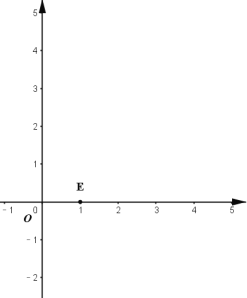
ЃЈ1ЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФАыГЄдВЕФУцЛ§ЮЊ__________ЃЛЯТСаИїЕу
ЕФАыГЄдВЕФУцЛ§ЮЊ__________ЃЛЯТСаИїЕу![]() ЁЂ
ЁЂ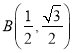 ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌФмБЛЕу
ЃЌФмБЛЕу![]() АыГЄВЖЛёЕФЕуга__________ЃЛ
АыГЄВЖЛёЕФЕуга__________ЃЛ
ЃЈ2ЃЉвбжЊЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЂйШчЭМЃЌЕу
ЃЌЂйШчЭМЃЌЕу![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЯпЖЮ
ЪБЃЌЯпЖЮ![]() ЩЯЕФЫљгаЕуОљПЩвдБЛЕу
ЩЯЕФЫљгаЕуОљПЩвдБЛЕу![]() АыГЄВЖЛёЃЌЧѓ
АыГЄВЖЛёЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛЂкШєЖдгкЦНУцЩЯЕФШЮвтЕуЃЈдЕуГ§ЭтЃЉЖМВЛФмАыГЄВЖЛёЯпЖЮ
ЕФШЁжЕЗЖЮЇЃЛЂкШєЖдгкЦНУцЩЯЕФШЮвтЕуЃЈдЕуГ§ЭтЃЉЖМВЛФмАыГЄВЖЛёЯпЖЮ![]() ЩЯЕФЫљгаЕуЃЌжБНгаДГі
ЩЯЕФЫљгаЕуЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпl1ЃКy=Љ![]() xгыЗДБШР§КЏЪ§y=
xгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBзѓВрЃЉЃЌвбжЊAЕуЕФзнзјБъЪЧ2ЃК
ЕФЭМЯѓНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBзѓВрЃЉЃЌвбжЊAЕуЕФзнзјБъЪЧ2ЃК
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉНЋжБЯпl1ЃКy=Љ![]() xЯђЩЯЦНвЦКѓЕФжБЯпl2гыЗДБШР§КЏЪ§y=
xЯђЩЯЦНвЦКѓЕФжБЯпl2гыЗДБШР§КЏЪ§y=![]() дкЕкЖўЯѓЯоФкНЛгкЕуCЃЌШчЙћЁїABCЕФУцЛ§ЮЊ30ЃЌЧѓЦНвЦКѓЕФжБЯпl2ЕФКЏЪ§БэДяЪНЃЎ
дкЕкЖўЯѓЯоФкНЛгкЕуCЃЌШчЙћЁїABCЕФУцЛ§ЮЊ30ЃЌЧѓЦНвЦКѓЕФжБЯпl2ЕФКЏЪ§БэДяЪНЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃПЊеЙЁАЪщЯуаЃдАЁБЛюЖЏвдРДЃЌЪмЕНЭЌбЇУЧЕФЙуЗКЙизЂЃЌбЇаЃЮЊСЫНтШЋаЃбЇЩњПЮЭтдФЖСЕФЧщПіЃЌЫцЛњЕїВщСЫВПЗжбЇЩњдквЛжмФкНшдФЭМЪщЕФДЮЪ§ЃЌВЂжЦГЩШчЭМВЛЭъећЕФЭГМЦБэ
бЇЩњНшдФЭМЪщЕФДЮЪ§
НшдФЭМЪщЕФДЮЪ§ | 0ДЮ | 1ДЮ | 2ДЮ | 3ДЮ | 4ДЮМАвдЩЯ |
ШЫЪ§ | 7 | 13 | a | 10 | 3 |
бЇЩњНшдФЭМЪщЕФДЮЪ§ЭГМЦБэ

ЧыФуИљОнЭГМЦЭМБэЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉa= ЃЛb=
ЃЈ2ЃЉИУЕїВщЭГМЦЪ§ОнЕФжаЮЛЪ§ЪЧ__________ДЮ
ЃЈ3ЃЉЩШаЮЭГМЦЭМжаЃЌЁА3ДЮЁБЫљЖдгІЕФЩШаЮдВаФНЧЖШЪ§ЪЧ______________ЃЛ
ЃЈ4ЃЉШєИУаЃЙВга2000УћбЇЩњЃЌИљОнЕїВщНсЙћЃЌЙРМЦИУаЃбЇЩњдквЛжмФкНшдФЭМЪщЁА4ДЮвдЩЯЁБЕФШЫЪ§
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪ§бЇЁАзлКЯгыЪЕМљЁБаЁзщЕФЭЌбЇАбЁАВтСПаБРЫїЖЅЖЫЕНЧХУцЕФОрРыЁБзїЮЊвЛЯюПЮЬтЛюЖЏЃЌЫћУЧжЦЖЉСЫВтСПЗНАИЃЌВЂРћгУПЮгрЪБМфНшжњИУЧХаБРЫїЭъГЩСЫЪЕЕиВтСПЃЎВтСПНсЙћШчЯТЃКШчЭМЃЌСНВрзюГЄаБРЫї![]() ЃЌ
ЃЌ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЗжБ№гыЧХУцНЛгк
ЃЌЗжБ№гыЧХУцНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧвЕу
СНЕуЃЌЧвЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() дкЭЌвЛЪњжБЦНУцФкЃЎВтЕУ
дкЭЌвЛЪњжБЦНУцФкЃЎВтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() УзЃЌЧыАяжњИУаЁзщИљОнВтСПЪ§ОнЃЌЧѓаБРЫїЖЅЖЫЕу
УзЃЌЧыАяжњИУаЁзщИљОнВтСПЪ§ОнЃЌЧѓаБРЫїЖЅЖЫЕу![]() ЕН
ЕН![]() ЕФОрРыЃЎЃЈВЮПМЪ§ОнЃК
ЕФОрРыЃЎЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЃЉ
ЃЎЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
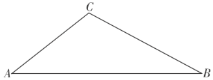
ЁОЬтФПЁПдкПЊЗЂЧјНЈЩшжаЃЌвЊВ№Г§бЬДбABЃЌдкЕиУцЩЯЪТЯШЛЖЈвдBЮЊдВаФЃЌАыОЖгыABЕШГЄЕФдВаЮЮЃЯеЧјЃЌЯждкДгРыBЕу21УздЖЕФНЈжўЮяCDЖЅЕуCЃЌВтЕУAЕуЕФбіНЧЮЊ![]() ЃЌBЕуЕФИЉНЧЮЊ
ЃЌBЕуЕФИЉНЧЮЊ![]() ЃЌЮЪРыBЕу35УздЖЕФЮФЮяБЃЛЄЧјЪЧЗёдкЮЃЯеЧјФкЃЌЧыЭЈЙ§МЦЫуЫЕУїЃЎ
ЃЌЮЪРыBЕу35УздЖЕФЮФЮяБЃЛЄЧјЪЧЗёдкЮЃЯеЧјФкЃЌЧыЭЈЙ§МЦЫуЫЕУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гы
гы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№ЯрНЛгк
жсЗжБ№ЯрНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌХзЮяЯп
СНЕуЃЌХзЮяЯп![]()
![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌНЛ
ЃЌНЛ![]() жсе§АыжсгкЕу
жсе§АыжсгкЕу![]() ЃЎ
ЃЎ
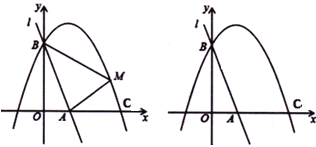
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉвбжЊЕу![]() ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌВЂЧвЕу
ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌВЂЧвЕу![]() дкЕквЛЯѓЯоФкЃЌСЌНг
дкЕквЛЯѓЯоФкЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§БэДяЪНЃЌВЂЧѓГі
ЕФКЏЪ§БэДяЪНЃЌВЂЧѓГі![]() ЕФзюДѓжЕМАДЫЪБЖЏЕу
ЕФзюДѓжЕМАДЫЪБЖЏЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉНЋЕу![]() ШЦдЕуа§зЊЕУЕу
ШЦдЕуа§зЊЕУЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌдка§зЊЙ§ГЬжаЃЌвЛЖЏЕу
ЃЌдка§зЊЙ§ГЬжаЃЌвЛЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌбиЯпЖЮ
ГіЗЂЃЌбиЯпЖЮ![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛЕФЫйЖШдЫЖЏЕН
ИіЕЅЮЛЕФЫйЖШдЫЖЏЕН![]() ЃЌдйбиЯпЖЮ
ЃЌдйбиЯпЖЮ![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЕН
ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЕН![]() КѓЭЃжЙЃЌЧѓЕу
КѓЭЃжЙЃЌЧѓЕу![]() дкећИідЫЖЏЙ§ГЬжагУЪБзюЩйЪЧЖрЩйЃП
дкећИідЫЖЏЙ§ГЬжагУЪБзюЩйЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЖдШЫГЩГЄЕФгАЯьЪЧОоДѓЕФЃЌвЛБОКУЪщЭљЭљФмИФБфШЫЕФвЛЩњЃЌУПФъЕФ4дТ23ШеБЛСЊКЯЙњНЬПЦЮФзщжЏШЗЖЈЮЊЁАЪРНчЖСЪщШеЁБЃЎРЖЬьжабЇЮЊСЫНтАЫФъМЖбЇЩњБОбЇЦкЕФПЮЭтдФЖСЧщПіЃЌЫцЛњГщВщВПЗжбЇЩњЖдЦфПЮЭтдФЖССПНјааЭГМЦЗжЮіЃЌЛцжЦГЩСНЗљВЛЭъећЕФЭГМЦЭМЃЎИљОнЭМЪОаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
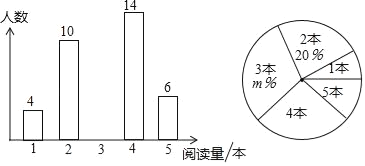
ЃЈ1ЃЉЧѓБЛГщВщбЇЩњШЫЪ§ЃЌПЮЭтдФЖССПЕФжкЪ§ЃЌЩШаЮЭГМЦЭМжаmЕФжЕЃЛВЂНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉШєЙцЖЈЃКБОбЇЦкдФЖС3БОвдЩЯЃЈКЌ3БОЃЉПЮЭтЪщМЎепЮЊЭъГЩФПБъЃЌОнДЫЙРМЦИУаЃ600УћбЇЩњжаФмЭъГЩДЫФПБъЕФгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com