
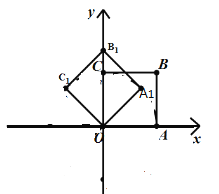
【题目】如图,在平面直角坐标系中,将正方形![]() 绕点
绕点![]() 逆时针旋转45°后得到正方形
逆时针旋转45°后得到正方形![]() .依此方式,绕点
.依此方式,绕点![]() 连续旋转2020次,得到正方形
连续旋转2020次,得到正方形![]() ,如果点
,如果点![]() 的坐标为
的坐标为![]() ,那么点
,那么点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据图形可知:点B在以O为圆心,以OB为半径的圆上运动,由旋转可知:将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,可得对应点B的坐标,根据规律发现是8次一循环,可得结论.
解:∵四边形OABC是正方形,且OA=![]() ,
,
∴A1(![]() ,
,![]() ),
),
如图,
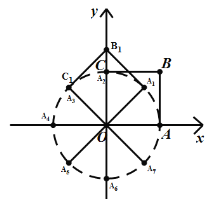
由旋转得:OA=OA1=OA2=OA3=…=![]() ,
,
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,
相当于将线段OA绕点O逆时针旋转45°,依次得到∠AOA1=∠A1OA2=∠A2OA3=…=45°,
∴A1(1,1),A2(0,![]() ),A3(
),A3(![]() ,
,![]() ),A4(
),A4(![]() ,0)…,
,0)…,
发现是8次一循环,所以2020÷8=252…余4,
∴点A2020的坐标为(![]() ,0);
,0);
故选:A.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
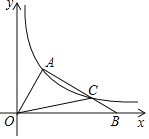
【题目】如图,在平面直角坐标系xOy中,△OAB的边OB在x轴上,过点A的反比例函数y=![]() 的图象交AB于点C,且AC:CB=2:1,S△OAC=
的图象交AB于点C,且AC:CB=2:1,S△OAC=![]() ,则k的值为( )
,则k的值为( )
A.![]() B.
B.![]() C.2D.2
C.2D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过原点的抛物线与![]() 轴交于另一点
轴交于另一点![]() ,抛物线顶点
,抛物线顶点![]() 的坐标为
的坐标为![]() ,其对称轴交
,其对称轴交![]() 轴于点
轴于点![]() .
.
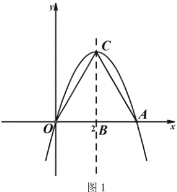
(1)求抛物线的解析式;
(2)如图2,点![]() 为抛物线上位于第一象限内且在对称轴右侧的一个动点,求使
为抛物线上位于第一象限内且在对称轴右侧的一个动点,求使![]() 面积最大时点
面积最大时点![]() 的坐标;
的坐标;
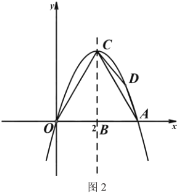
(3)在对称轴上是否存在点![]() ,使得点
,使得点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 满足以点
满足以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形.若存在,请求出点
为顶点的四边形为菱形.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中央电视台《朗读者》节目的播出,“朗读”为越来越多的同学所喜爱,西宁市某中学计划在全校开展“朗读”活动,为了了解同学们对这项活动的参与态度,随机对部分学生进行了一次调查,调查结果整理后,将这部分同学的态度划分为四个类别:![]() .积极参与,
.积极参与,![]() .一定参与,
.一定参与,![]() .可以参与,
.可以参与,![]() .不参与.根据调查结果制作了如下不完整的统计表和统计图.
.不参与.根据调查结果制作了如下不完整的统计表和统计图.
学生参与“朗读”的态度统计表
类别 | 人数 | 所占百分比 |
| 18 |
|
| 20 |
|
|
|
|
| 4 |
|
合计 |
|
|
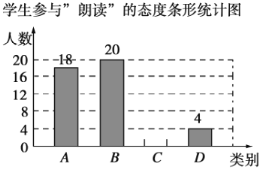
请你根据以上信息,解答下列问题:
(1)![]() ______,
______,![]() ______,并将条形统计图补充完整;
______,并将条形统计图补充完整;
(2)该校有1500名学生,如果“不参与”的人数不超过150人时,“朗读”活动可以顺利开展,通过计算分析这次活动能否顺利开展?
(3)“朗读”活动中,九年级一班比较优秀的四名同学恰好是两男两女,从中随机选取两人在班级进行朗读示范,试用画树状图法或列表法求所选两人都是女生的概率,并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
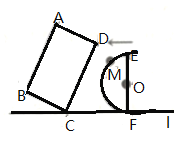
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() 与直线
与直线![]() 相交所得的锐角为60°.点
相交所得的锐角为60°.点![]() 在直线
在直线![]() 上,
上,![]() ,
,![]() 直线
直线![]() ,垂足为点
,垂足为点![]() 且
且![]() ,以
,以![]() 为直径,在
为直径,在![]() 的左侧作半圆
的左侧作半圆![]() ,点
,点![]() 是半圆
是半圆![]() 上任一点.
上任一点.
发现:![]() 的最小值为_________,
的最小值为_________,![]() 的最大值为__________,
的最大值为__________,![]() 与直线
与直线![]() 的位置关系_________.
的位置关系_________.
思考:矩形![]() 保持不动,半圆
保持不动,半圆![]() 沿直线
沿直线![]() 向左平移,当点
向左平移,当点![]() 落在
落在![]() 边上时,求半圆与矩形重合部分的周长和面积.
边上时,求半圆与矩形重合部分的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
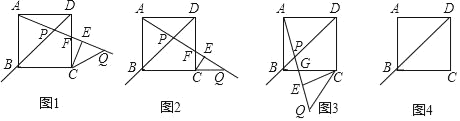
【题目】合与实践﹣﹣探究图形中角之间的等量关系及相关问题.
问题情境:
正方形ABCD中,点P是射线DB上的一个动点,过点C作CE⊥AP于点E,点Q与点P关于点E对称,连接CQ,设∠DAP=α(0°<α<135°),∠QCE=β.
初步探究:
(1)如图1,为探究α与β的关系,勤思小组的同学画出了0°<α<45°时的情形,射线AP与边CD交于点F.他们得出此时α与β的关系是β=2α.借助这一结论可得当点Q恰好落在线段BC的延长线上(如图2)时,α= °,β= °;
深入探究:
(2)敏学小组的同学画出45°<α<90°时的图形如图3,射线AP与边BC交于点G.请猜想此时α与β之间的等量关系,并证明结论;
拓展延伸:
(3)请你借助图4进一步探究:①当90°<α<135°时,α与β之间的等量关系为 ;
②已知正方形边长为2,在点P运动过程中,当α=β时,PQ的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区在实施居民用水管理前,随机调查了部分家庭(单位:户)去年的月均用水量(单位:t),并将调查数据进行整理,绘制出如下不完整的统计图表:
月均用水量 | 频数 | 频率 |
0≤x<5 | 6 | 12% |
5≤x<10 | 12 | 24% |
10≤x<15 |
| 32% |
15≤x<20 | 10 | 20% |
20≤x<25 | 4 |
|
25≤x<30 | 2 | 4% |
合计 |
| 100% |
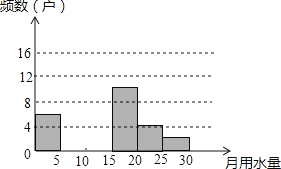
请解答以下问题:
(I)把上面的频数分布表和频数分布直方图补充完整;
(Ⅱ)若该小区有2000户家庭,根据此次随机抽查的数据估计,该小区月均用水量不低于20t的家庭有多少户?
(Ⅲ)为了鼓励节约用水,要确定一个月均用水量的标准,超出该标准的部分按1.5倍价格收费,若要使68%的家庭水费支出不受影响,那么,你觉得家庭月均用水量应定为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com