
【题目】如图,在边长为2的正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为边
为边![]() 上一动点,设
上一动点,设![]() ,线段
,线段![]() 的垂直平分线分别交边
的垂直平分线分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .
.
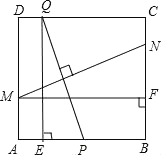
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)顺次连接![]() 、
、![]() 、
、![]() 、
、![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,求出
,求出![]() 与自变量
与自变量![]() 之间的函数关系式,并求
之间的函数关系式,并求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)![]() ,
,![]() 的最小值为2
的最小值为2
【解析】
(1)由四边形![]() 是正方形得到
是正方形得到![]() ,
,![]() ,又由
,又由![]() ,利用ASA即可证得;
,利用ASA即可证得;
(2)分为两种情况:①当![]() 在
在![]() 上时,由点
上时,由点![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,又由勾股定理求得
,又由勾股定理求得![]() ,由
,由![]() 得到
得到![]() 的值,又
的值,又![]() 求得面积
求得面积![]() ,由
,由![]() 范围得到
范围得到![]() 的最小值;②当
的最小值;②当![]() 在
在![]() 上时,同法可求
上时,同法可求![]() 的最小值.
的最小值.
解:(1)证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 、
、![]() 都是矩形,
都是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴MF=QE
又∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
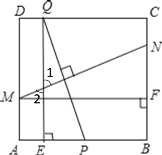
(2)解:分为两种情况:①当![]() 在
在![]() 上时,
上时,
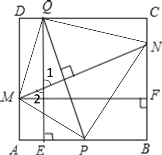
∵点![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
由勾股定理,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵0≤AE≤AP
∴![]() ,
,
∴当![]() 时,
时,![]() .
.
②当![]() 在
在![]() 上时,
上时,
∵点![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
由勾股定理,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵AP≤AE≤AB
∴![]() ,
,
∴当![]() 时,
时,![]() .
.
综上:![]() ,
,![]() 的最小值为2.
的最小值为2.


科目:初中数学 来源: 题型:
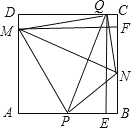
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 是等边三角形,
是等边三角形,![]() 为对角线
为对角线![]() (不含
(不含![]() 点)上任意一点,将
点)上任意一点,将![]() 绕点
绕点![]() 逆时针旋转60°得到
逆时针旋转60°得到![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
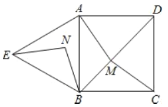
(1)求证![]() ;
;
(2)①当![]() 点在何处时,
点在何处时,![]() 的值最小;
的值最小;
②当![]() 点在何处时,
点在何处时,![]() 的值最小,并说明理由;
的值最小,并说明理由;
(3)当![]() 的最小值为
的最小值为![]() 时,求正方形的边长.
时,求正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北盘江大桥坐落于云南宜威与贵州水城交界处,横跨云贵两省,为目前世界第一高桥图1是大桥的实物图,图2是从图1中引申出的平面图,测得桥护栏BG=1.8米,拉索AB与护栏的夹角是26°,拉索ED与护栏的夹角是60°,两拉索底端距离BD为300m,若两拉索顶端的距离AE为90m,请求出立柱AH的长.(tan26°≈0.5,sin26°≈0.4,![]() 1.7)
1.7)
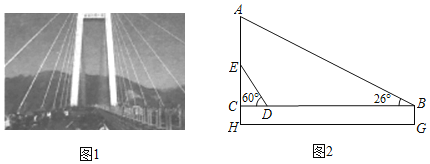
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列18×7的网格中,横、纵坐标均为整数的点叫做格点,例如A(﹣8,0)、B(﹣4.3)都是格点.
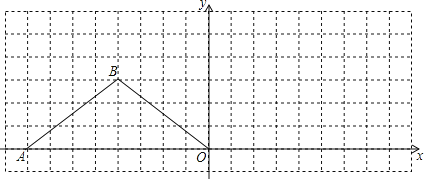
(1)直接写出△ABO的形状:
(2)要求在图中仅用无刻的直尺画图:将△ABO绕点O顺时针旋转得△DEO,且点B的对应点E落在x轴正半轴上.
操作如下:
第一步:在x正半轴上找一个格点E,使OE=OB;
第二步:找一个格点F,使∠EOF=∠AOB;
第三步:找一个格点M,作直线AM交直线OF于D,连DE,则△DEO即为所作出的图形.请你按以上操作完成画图.并直接写出点E,F,M三点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
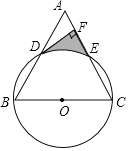
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 与
与![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求抛物线的解析式;
(2)如图1,点![]() 是抛物线上(
是抛物线上(![]() 轴下方)的一个动点,过点
轴下方)的一个动点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() 试判断在点
试判断在点![]() 运动过程中,以点
运动过程中,以点![]() 为顶点的四边形能否构成平行四边形,若能,请求出点
为顶点的四边形能否构成平行四边形,若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
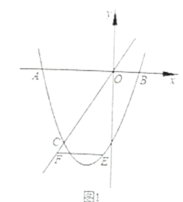
(3)如图2,点![]() 是抛物线的顶点,抛物线的对称轴
是抛物线的顶点,抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() 当点
当点![]() 在抛物线上
在抛物线上![]() 之间运动时,连接
之间运动时,连接![]() 交
交![]() 于点
于点![]() 连接
连接![]() 并延长交
并延长交![]() 于点
于点![]() 猜想在点
猜想在点![]() 的运动过程中,
的运动过程中,![]() 的和是否为定值?若是,试求出该定值;若不是,请说明理由.
的和是否为定值?若是,试求出该定值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有6个白色乒乓球和若干个红色的乒乓球,这些球除颜色外其余均相同,搅拌均匀后,从这个袋子里随机摸出一个乒乓球,是红球的概率是![]()
(1)求该袋子中红球的个数;
(2)小亮取出3个白色乒乓球分别表上1,2,3个数字,装入另一个不透明的袋子里搅拌均匀,第一次从袋子里摸出一个球并记录下该球上的数字,重新放回袋子中搅拌均匀,第二次从袋子中摸出一个球并记录下该球上的数字,求这两个数字之积是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与双曲线
与双曲线![]() 只有一个交点A(1,2),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,
只有一个交点A(1,2),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,
求:(1)直线、双曲线的解析式.
(2)线段BC的长;
(3)三角形BOC的内心到三边的距离.
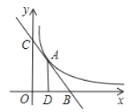
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com