
【题目】如图,点![]() 在函数
在函数![]() 的图象上,直线
的图象上,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,且点
,且点![]() 的横坐标为4,点
的横坐标为4,点![]() 的纵坐标为
的纵坐标为![]() ,则
,则![]() 的面积是________.
的面积是________.

【答案】![]()
【解析】
作EC⊥x轴于C,EP⊥y轴于P,FD⊥x轴于D,FH⊥y轴于H,由题意可得点A,B的坐标分别为(4,0),B(0,![]() ),利用待定系数法求出直线AB的解析式,再联立反比例函数解析式求出点,F的坐标.由于S△OEF+S△OFD=S△OEC+S梯形ECDF,S△OFD=S△OEC=1,所以S△OEF=S梯形ECDF,然后根据梯形面积公式计算即可.
),利用待定系数法求出直线AB的解析式,再联立反比例函数解析式求出点,F的坐标.由于S△OEF+S△OFD=S△OEC+S梯形ECDF,S△OFD=S△OEC=1,所以S△OEF=S梯形ECDF,然后根据梯形面积公式计算即可.
解:如图,作EP⊥y轴于P,EC⊥x轴于C,FD⊥x轴于D,FH⊥y轴于H,
由题意可得点A,B的坐标分别为(4,0),B(0,![]() ),
),
由点B的坐标为(0,![]() ),设直线AB的解析式为y=kx+
),设直线AB的解析式为y=kx+![]() ,将点A的坐标代入得,0=4k+
,将点A的坐标代入得,0=4k+![]() ,解得k=-
,解得k=-![]() .
.
∴直线AB的解析式为y=-![]() x+
x+![]() .
.
联立一次函数与反比例函数解析式得,
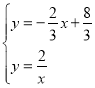 ,解得
,解得![]() 或
或![]() ,
,
即点E的坐标为(1,2),点F的坐标为(3,![]() ).
).
∵S△OEF+S△OFD=S△OEC+S梯形ECDF,而S△OFD=S△OEC=![]() ×2=1,
×2=1,
∴S△OEF=S梯形ECDF=![]() ×(AF+CE)×CD=
×(AF+CE)×CD=![]() ×(
×(![]() +2)×(3-1)=
+2)×(3-1)=![]() .
.
故答案为:![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠ABC=90°,AB=BC=2,现将Rt△ABC绕点A逆时针旋转30°得到△AED,则图中阴影部分的面积是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是抛物线上在第一象限内的一个动点,且点
是抛物线上在第一象限内的一个动点,且点![]() 的横坐标为
的横坐标为![]() .
.
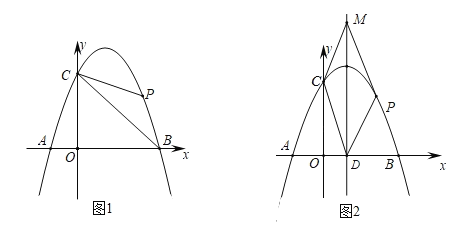
(1)求抛物线的表达式;
(2)如图1,连接![]() ,
,![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数表达式,并求出当
的函数表达式,并求出当![]() 为何值时,
为何值时,![]() 的面积
的面积![]() 有最大值;
有最大值;
(3)如图2,设抛物线的对称轴为直线![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() .在直线
.在直线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形?若存在,求出点
是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
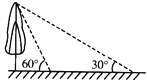
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年重庆国际马拉松赛于3月31日在南滨公园鸣枪开跑已知A、B两补给站之间的路程为1470米,志愿者甲、乙都从A站出发支援B站.甲先出发,且在途中停留了4分钟,甲出发6分钟后,乙才从A站出发.在整个行走过程中,两人保持各自速度匀速行走,两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达B站时,甲与B站相距的路程是_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
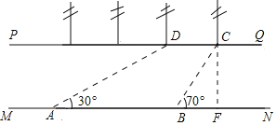
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com