
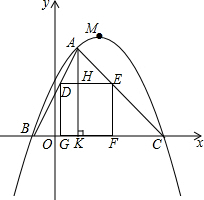
 ��ͼ����ƽ��ֱ������ϵxOy�У���MΪ�������������x��ֱ��ཻ��B��C���㣬��������һ��A�ĺ�����Ϊ2������AB��AC��������DEFG��һ��GF���߶�BC�ϣ���D��E���߶�AB��AC�ϣ�AK��x���ڵ�K����DE�ڵ�H���±������������������ϲ��ֵ㣨x��y��������ֵ��
��ͼ����ƽ��ֱ������ϵxOy�У���MΪ�������������x��ֱ��ཻ��B��C���㣬��������һ��A�ĺ�����Ϊ2������AB��AC��������DEFG��һ��GF���߶�BC�ϣ���D��E���߶�AB��AC�ϣ�AK��x���ڵ�K����DE�ڵ�H���±������������������ϲ��ֵ㣨x��y��������ֵ��| x | �� | -2 | 0 | 4 | 8 | 10 | �� |
| y | �� | 0 | 5 | 9 | 5 | 0 | �� |
���� ��1��������֪���������ݽ�϶���ʽֱ����������߽���ʽ���ɣ�
��2�����ȵó��ı���HEFKΪ���Σ������á�ADE�ס�ABC���ó�������DEFG�ı߳���
��3���������AB����ֱ�߽���ʽ�������ó�D�����꣬�����ֱ��A��D��Ľ���ʽ�ó�Q������꼴�ɣ�
��� �⣺��1����ͼ���ɵã������ߵĶ�������Ϊ����4��9����
�躯������ʽΪ��y=a��x-4��2+9��a��0����
�ѵ㣨0��5������y=a��x-4��2+9��
��ã�a=-$\frac{1}{4}$��
�ຯ������ʽΪ��y=-$\frac{1}{4}$��x-4��2+9��
��2����������DEFG�ı߳�Ϊm��
��AK��x�ᣬ
���AKC=90�㣬
�ߡ�DEF=��EFG=90�㣬
���ı���HEFKΪ���Σ�
��HK=EF=m��
�ߵ�A��������y=-$\frac{1}{4}$��x-4��2+9�ϣ�������Ϊ2��
��y=-$\frac{1}{4}$��x-4��2+9=8��
���A����������2��8����
��AK=8����AH=AK-HK=8-m��
������ɵã�B��-2��0����C��10��0����
��BC=12��
��DE��BC��
���ADE�ס�ABC��
��$\frac{AH}{AK}$=$\frac{DE}{BC}$��
��$\frac{8-m}{8}$=$\frac{m}{12}$��
��m=$\frac{24}{5}$��
�������εı߳�Ϊ��$\frac{24}{5}$��
��3�����ڣ�
���ɣ�������M�������ߵĶԳ���ֱ��l��x=4��
���A����ֱ��l��x=4�ԳƵ�ΪA�䣬A��������Ϊ����6��8����
����AB����ֱ�߽���ʽΪ��y=kx+b��
��$\left\{\begin{array}{l}{8=2k+b}\\{0=-2k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$��
��AB����ֱ�߽���ʽΪ��y=2x+4��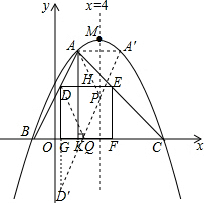
��D��ֱ��AB�ϣ�DG=$\frac{24}{5}$��
���D����������$\frac{24}{5}$��
��2x+4=$\frac{24}{5}$��
��ã�x=$\frac{2}{5}$��
���D����������$\frac{2}{5}$��$\frac{24}{5}$����
���D����x��ԳƵ�ΪD�䣬��D�䣨$\frac{2}{5}$��-$\frac{24}{5}$����
����A��D�佻�Գ����ڵ�P����x���ڵ�Q������AP��DQ��
���ı���ADQP���ܳ���С��
��ֱ��A��D��Ľ���ʽΪ��y=k��x+b�䣬
��$\left\{\begin{array}{l}{6k��+b��=8}\\{\frac{2}{5}k��+b��=-\frac{24}{5}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k��=\frac{16}{7}}\\{b��=-\frac{40}{7}}\end{array}\right.$��
��ֱ��A��D��Ľ���ʽΪ��y=$\frac{16}{7}$x-$\frac{40}{7}$��
��x=4ʱ��y=$\frac{16}{7}$��4-$\frac{40}{7}$=$\frac{24}{7}$����P��4��$\frac{24}{7}$����
��y=0ʱ��x=$\frac{5}{2}$��
��Q����������$\frac{5}{2}$��0����
���� ������Ҫ�����˶��κ����ۺ��Լ�����ϵ������һ�κ�������ʽ��֪ʶ��������ԳƵó��ı���ADQP���ܳ���СʱP��λ���ǽ���ؼ���


 С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д� ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��10 | B�� | 10��a��12 | C�� | 10��a��12 | D�� | 10��a��12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �˽����Ա�����Ĵ����Ӧʹ�ó������� | |
| B�� | һ������3��6��6��7��9����λ����6 | |
| C�� | ��2000��ѧ����ѡ200��ѧ�����г������飬��������Ϊ2000 | |
| D�� | ��һö�ʵؾ��ȵ�Ӳ�ң����泯���DZ�Ȼ�¼� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
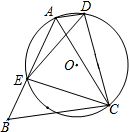 ��֪��ͼ����ACD�ڽ��ڡ�O��EΪ��O��һ�㣬��ED=EC������C��BC��AD��AE���ӳ����ڵ�B����cosB=$\frac{3}{5}$��BC=2BE��AE=7����ED=$\sqrt{65}$��
��֪��ͼ����ACD�ڽ��ڡ�O��EΪ��O��һ�㣬��ED=EC������C��BC��AD��AE���ӳ����ڵ�B����cosB=$\frac{3}{5}$��BC=2BE��AE=7����ED=$\sqrt{65}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
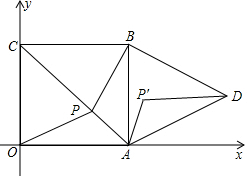 ��ͼ��������ABCO�ı߳�Ϊ1������A��C�ֱ���x��y���ϣ���ABΪ���������ȱ�������ADB����PΪ�Խ���AC�ϵĶ��㣮
��ͼ��������ABCO�ı߳�Ϊ1������A��C�ֱ���x��y���ϣ���ABΪ���������ȱ�������ADB����PΪ�Խ���AC�ϵĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
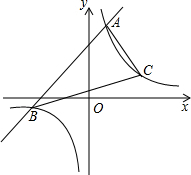 ��֪һ�κ���y1=x+m��ͼ���뷴��������y2=$\frac{6}{x}$��ͼ����A��B���㣬��֪��x��1ʱ��y1��y2����0��x��1ʱ��y1��y2��
��֪һ�κ���y1=x+m��ͼ���뷴��������y2=$\frac{6}{x}$��ͼ����A��B���㣬��֪��x��1ʱ��y1��y2����0��x��1ʱ��y1��y2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com