
【题目】在正方形![]() 中,点
中,点![]() 是直线
是直线![]() 上动点,以
上动点,以![]() 为边作正方形
为边作正方形![]() ,
,![]() 所在直线与
所在直线与![]() 所在直线交于点
所在直线交于点![]() ,连接
,连接![]() .
.
(1)如图1,当点![]() 在
在![]() 边上时,延长
边上时,延长![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
②若![]() ,求
,求![]() 的值;
的值;
(2)当正方形![]() 的边长为4,
的边长为4,![]() 时,请直接写出
时,请直接写出![]() 的长.
的长.

【答案】(1)①证明见解析;②![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)通过正方形的性质和等量代换可得到![]() ,从而可用SAS证明
,从而可用SAS证明![]() ,利用全等的性质即可得出
,利用全等的性质即可得出![]() ;
;
(2)先证明![]() ,则有
,则有![]() ,进而可证明
,进而可证明![]() ,得到
,得到![]() ,再利用
,再利用![]() 得出
得出![]() ,作
,作![]() 交EH于点P,则
交EH于点P,则![]() ,利用相似三角形的性质得出
,利用相似三角形的性质得出![]() ,则问题可解;
,则问题可解;
(3)设![]() ,则
,则![]() ,表示出EH,然后利用
,表示出EH,然后利用![]() 解出x的值,进而可求EH的长度;当E在BA的延长线上时,画出图形,用同样的方法即可求EH的长度.
解出x的值,进而可求EH的长度;当E在BA的延长线上时,画出图形,用同样的方法即可求EH的长度.
(1)①证明:∵四边形ABCD,DEFG都是正方形
∴![]()
∵![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
②∵四边形DEFG是正方形
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
∵![]()
![]()
![]()
作![]() 交EH于点P,则
交EH于点P,则![]()

![]()
![]()

(3)当点E在AB边上时,
设![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
![]()
解得![]()
∴![]()
当E在BA的延长线上时,如下图

∵四边形ABCD,DEFG都是正方形
∴![]()
∵![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
∴点G在BC边上
∵四边形DEFG是正方形
![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
设![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
解得![]()
∴![]()
综上所述,EH的长度为![]() 或
或![]() .
.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0.
(1)试判断原方程根的情况;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.
(友情提示:AB=|x2﹣x1|)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂接的600件玩具的订单后,决定由甲、乙两车间共同完成生产任务,已知甲车间工作效率是乙车间的2倍,乙车间单独完成此项生产任务比甲车间单独完成多用10天.
(1)求甲,乙两车间平均每天各能制作多少件玩具;
(2)两车间同时开工3天后,临时又增加了90件的玩具生产任务,为了使完成任务的总时间不超过7天,两车间从第4天起各自提高工作效率,提高工作效率后甲车间工作效率仍是乙车间工作率的2倍,求乙车间提高效率后每天至少生产多少件玩具.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点.
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积和周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 内接于⊙
内接于⊙![]() ,
,![]() 是直径,
是直径,![]() ,点
,点![]() 在⊙
在⊙![]() 上.
上.
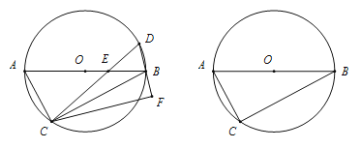
(1)如图,若弦![]() 交直径
交直径![]() 于点
于点![]() ,连接
,连接![]() ,线段
,线段![]() 是点
是点![]() 到
到![]() 的垂线.
的垂线.
①问![]() 的度数和点
的度数和点![]() 的位置有关吗?请说明理由.
的位置有关吗?请说明理由.
②若![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,求
倍,求![]() 的正弦值.
的正弦值.
(2)若⊙![]() 的半径长为
的半径长为![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,面积为150.
,面积为150.

(1)尺规作图:作![]() 的平分线交
的平分线交![]() 于点
于点![]() ;(不要求写作法,保留作图痕迹)
;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,求出点![]() 到两条直角边的距离.
到两条直角边的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直
,对称轴为直![]() .下列结论:
.下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 若点
若点![]() 点
点![]() 点
点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() .其中正确的结论有( )
.其中正确的结论有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义: 对于平面直角坐标系xOy上的点P(a, b) 和抛物线![]() , 我们称P(a, b)是抛物线
, 我们称P(a, b)是抛物线![]() 的相伴点, 抛物线
的相伴点, 抛物线![]() 是点P(a, b) 的相伴抛物线.
是点P(a, b) 的相伴抛物线.
如图,已知点A(-2, -2),B(4, -2),C(1, 4).
(1) 点A的相伴抛物线的解析式为 ;过A, B两点的抛物线![]() 的相伴点坐标为 ;
的相伴点坐标为 ;
(2) 设点P(a, b) 在直线AC上运动:
①点P(a, b)的相伴抛物线的顶点都在同一条抛物线Ω上, 求抛物线Ω的解析式.
②当点P(a, b)的相伴抛物线的顶点落在△ABC 内部时, 请直接写出 a 的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com