
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЮЊзјБъдЕуЃЌЕу
ЮЊзјБъдЕуЃЌЕу![]() ЮЊЕквЛЯѓЯоФквЛЕуЃЌЕу
ЮЊЕквЛЯѓЯоФквЛЕуЃЌЕу![]() дк
дк![]() жсе§АыжсЩЯЃЌЧв
жсе§АыжсЩЯЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЖЏЕу![]() вдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЃЌДгЕу
вдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЃЌДгЕу![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() жсе§АыжсдШЫйдЫЖЏЃЌЩшЕу
жсе§АыжсдШЫйдЫЖЏЃЌЩшЕу![]() ЕФдЫЖЏЪБМфЮЊ
ЕФдЫЖЏЪБМфЮЊ![]() УыЃЌ
УыЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧыгУКЌга
ЃЌЧыгУКЌга![]() ЕФЪНзгБэЪО
ЕФЪНзгБэЪО![]() ЃЌВЂжБНгаДГі
ЃЌВЂжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпНЛ
жсЕФДЙЯпНЛ![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЕФЦНааЯп
жсЕФЦНааЯп![]() ЃЌдкЕу
ЃЌдкЕу![]() ЕФдЫЖЏЙ§ГЬжаЃЌжБЯп
ЕФдЫЖЏЙ§ГЬжаЃЌжБЯп![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЪЧвд
ЪЧвд![]() ЮЊбќЕФЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕу
ЮЊбќЕФЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕу![]() зјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
зјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ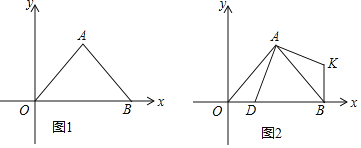
ЁОД№АИЁПЃЈ1ЃЉЃЈ10ЃЌ0ЃЉЃЛЃЈ2ЃЉS=25-5tЃЈ0ЃМtЁм5ЃЉЛђS=5t-25ЃЈtЃО5ЃЉЃЛЃЈ3ЃЉДцдкЃЌЃЈ5ЃЌ5ЃЉЛђЃЈ3ЃЌ5ЃЉЛђЃЈ17ЃЌ5ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉзїAMЁЭOBгкMЃЌзѓВрЁїOABЪЧЕШбќжБНЧШ§НЧаЮЃЌЕУГіЁЯOAB=90ЁуЃЌЁЯABO=45ЁуЃЌBM=OM=5ЃЌЧѓГіOB=10ЃЌМДПЩЕУГіЕуBЕФзјБъЃЛ
ЃЈ2ЃЉЗжСНжжЧщПіЬжТлЃКЕБ0ЃМtЁм5ЪБЃЌOP=2tЃЌдђPB=10-2tЃЛЕБtЃО5ЪБЃЌOP=2tЃЌдђPB=2t-10ЃЛгЩШ§НЧаЮУцЛ§ЙЋЪНМДПЩЕУГіНсЙћЃЛ
ЃЈ3ЃЉгЩASAжЄУїЁїOADЁеЁїBAKЃЌЕУГіOD=BK=2ЃЌЗжСНжжЧщПіЃКЕБЁЯPRK=90ЁуЪБЃЌЕуRгыAжиКЯЃЌЕУГіRЃЈ5ЃЌ5ЃЉЃЛЕБЁЯRPK=90ЁуЪБЃЌЂйЕБPдкBЕФзѓВрЪБЃЌзїREЁЭOBгкEЃЌжЄЕУЁїEPRЁеЁїBKPЃЌЕУГіEP=BK=2ЃЌRE=PB=5ЃЌЧѓГіOE=3МДПЩЃЛЂкЕБPдкBЕФгвВрЪБЃЌЭЌРэЕУГіЕуRЕФзјБъЮЊЃЈ17ЃЌ5ЃЉЃЌМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉзїAMЁЭOBгкMЃЌШчЭМ1ЫљЪОЃК
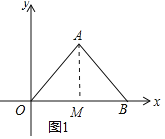
ЁпЁЯAOB=45ЁуЃЌOA=BAЃЌЕуAЃЈ5ЃЌ5ЃЉЃЌ
ЁрЁїOABЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯOAB=90ЁуЃЌ
ЁрЁЯABO=45ЁуЃЌBM=OM=5ЃЌ
ЁрOB=10ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ10ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉЕБ0ЃМtЁм5ЪБЃЌШчЭМ2ЫљЪОЃК
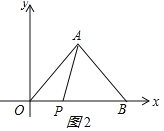
OP=2tЃЌдђPB=10-2tЃЌ
ЁрS=![]() ЃЈ10-2tЃЉЁС5=25-5tЃЛ
ЃЈ10-2tЃЉЁС5=25-5tЃЛ
ЕБtЃО5ЪБЃЌШчЭМ3ЫљЪОЃК
OP=2tЃЌдђPB=2t-10ЃЌ
ЁрS=![]() ЃЈ2t-10ЃЉЁС5=5t-25ЃЛ
ЃЈ2t-10ЃЉЁС5=5t-25ЃЛ
злЩЯЫљЪіЃКS=25-5tЃЈ0ЃМtЁм5ЃЉЛђS=5t-25ЃЈtЃО5ЃЉЃЛ
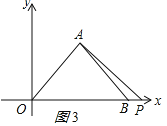
ЃЈ3ЃЉДцдкЃЌЁпAKЁЭADЃЌ
ЁрЁЯDAK=90Ёу=ЁЯOABЃЌ
ЁрЁЯOAD=ЁЯBAKЃЌ
ЁпBKЁЭOBЃЌ
ЁрЁЯABK=90Ёу-45Ёу=45ЁуЃЌ
дкЁїOADКЭЁїBAKжаЃЌ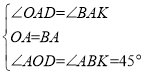 ЃЌ
ЃЌ
ЁрЁїOADЁеЁїBAKЃЈASAЃЉЃЌ

ЁрOD=BK=2ЃЌ
ЕБЁЯPRK=90ЁуЪБЃЌЕуRгыAжиКЯЃЌ
ЁрRЃЈ5ЃЌ5ЃЉЃЛ
ЕБЁЯRPK=90ЁуЪБЃЌ
ЂйЕБPдкBЕФзѓВрЪБЃЌШчЭМ4ЫљЪОЃК
зїREЁЭOBгкEЃЌЭЌРэжЄЕУЁїEPRЁеЁїBKPЃЌ

ЁрEP=BK=2ЃЌRE=PB=5ЃЌ
ЁрOE=10-5-2=3ЃЌ
ЁрRЃЈ3ЃЌ5ЃЉЃЛ
ЂкЕБPдкBЕФгвВрЪБЃЌШчЭМ5ЫљЪОЃК
ЭЌРэЕУГіЕуRЕФзјБъЮЊЃЈ17ЃЌ5ЃЉЃЛ
злЩЯЫљЪіЃКжБЯпaЩЯДцдкЕуRЃЌЪЙЁїPKRЪЧвдPRЮЊбќЕФЕШбќжБНЧШ§НЧаЮЃЌЕуRзјБъЮЊЃЈ5ЃЌ5ЃЉЛђЃЈ3ЃЌ5ЃЉЛђЃЈ17ЃЌ5ЃЉЃЎ/p>


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЕФЪЧгУЦхзгГЩЕФTзжаЮЭМАИ:
(1)ЬюаДЯТБэ:
ЭМАИађКХ | Ђй | Ђк | Ђл | Ђм | ЁЁ | Ђр |
УПИіЭМАИжаЦхзгЕФИіЪ§ | 5 | 8 | ЁЁ |
(2)Ек![]() ИіЁАTЁАзжаЮЭМАИжаЦхзгЕФИіЪ§ЮЊЖрЩй (гУКЌ
ИіЁАTЁАзжаЮЭМАИжаЦхзгЕФИіЪ§ЮЊЖрЩй (гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЛ
ЕФДњЪ§ЪНБэЪО)ЃЛ
(3)Ек20ИіЁАTЁБзжаЮЭМАИЙВгаЦхзгЖрЩйИі?
(4)МЦЫуЧА20ИіЁАTЁБзжаЮЭМАИжаЦхзгЕФзмИіЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊБэЪОЪЕЪ§aЃЌbЕФЕудкЪ§жсЩЯЕФЮЛжУШчЭМЫљЪОЃЌЯТСаНсТлДэЮѓЕФЪЧ( )
![]()
A. ![]() ЃМ1ЃМ
ЃМ1ЃМ![]() B. 1ЃМЃaЃМb C. 1ЃМ
B. 1ЃМЃaЃМb C. 1ЃМ![]() ЃМb D. ЃbЃМaЃМЃ1
ЃМb D. ЃbЃМaЃМЃ1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЫЕЗЈе§ШЗЕФИіЪ§гаЃЈ ЃЉ
ЂйЗНГЬ![]() ЕФЗЧИКећЪ§НтжЛга
ЕФЗЧИКећЪ§НтжЛга![]() ЃЛЂкгЩШ§ЬѕЯпЖЮЪзЮВЫГДЮСЌНгЫљзщГЩЕФЭМаЮНазіШ§НЧаЮЃЛЂлШчЙћ
ЃЛЂкгЩШ§ЬѕЯпЖЮЪзЮВЫГДЮСЌНгЫљзщГЩЕФЭМаЮНазіШ§НЧаЮЃЛЂлШчЙћ![]() ЃЌФЧУД
ЃЌФЧУД![]() ЪЧжБНЧШ§НЧаЮЃЛЂмИїБпЖМЯрЕШЕФЖрБпаЮЪЧе§ЖрБпаЮЃЛЂнШчЙћвЛИіШ§НЧаЮжЛгавЛЬѕИпдкШ§НЧаЮЕФФкВПЃЌФЧУДетИіШ§НЧаЮвЛЖЈЪЧЖлНЧШ§НЧаЮЃЎ
ЪЧжБНЧШ§НЧаЮЃЛЂмИїБпЖМЯрЕШЕФЖрБпаЮЪЧе§ЖрБпаЮЃЛЂнШчЙћвЛИіШ§НЧаЮжЛгавЛЬѕИпдкШ§НЧаЮЕФФкВПЃЌФЧУДетИіШ§НЧаЮвЛЖЈЪЧЖлНЧШ§НЧаЮЃЎ
A.0ИіB.1ИіC.2ИіD.3Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁППЊбЇГѕЃЌаЁЗМКЭаЁССШЅЩЬЕъЙКТђбЇЯАгУЦЗЃЌаЁЗМгУ30дЊЧЎЙКТђИжБЪЕФЪ§СПЪЧаЁССгУ25дЊЧЎЙКТђБЪМЧБОЪ§СПЕФ2БЖЃЌвбжЊУПжЇИжБЪЕФМлИёБШУПБОБЪМЧБОЕФМлИёЩй2дЊЃЎ
ЃЈ1ЃЉЧѓУПжЇИжБЪКЭУПБОБЪМЧБОИїЪЧЖрЩйдЊЃЛ
ЃЈ2ЃЉбЇаЃдЫЖЏЛсКѓЃЌАржїШЮФУГі200дЊбЇаЃНБРјЛљН№НЛИјаЁЗМЃЌдйДЮЙКТђЩЯЪіМлИёЕФИжБЪКЭБЪМЧБОЙВ48МўзїЮЊНБЦЗЃЌНБРјИјаЃдЫЖЏЛсжаБэЯжЭЛГіЕФЭЌбЇЃЌОЫЋЗНаЩЬЃЌЩЬЕъИјГігХЛнЪЧЙКТђЩЬЦЗЕФзмН№ЖюГЌГі50ЕФВПЗжИјДђОХелЃЌЧыЮЪаЁЗМжСЩйвЊТђЖрЩйжЇИжБЪЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуCЃЌEЃЌFЃЌBдкЭЌвЛжБЯпЩЯЃЌЕуAЃЌDдкBCвьВрЃЌABЁЮCDЃЌAE=DFЃЌЁЯA=ЁЯDЃЎ
ЃЈ1ЃЉЧѓжЄЃКAB=CDЃЛ
ЃЈ2ЃЉШєAB=CFЃЌЁЯB=30ЁуЃЌЧѓЁЯDЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+cгыxжсЯрНЛгкСНЕуAЃЈ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгыyжсЯрНЛгкЕуCЃЈ0ЃЌ3ЃЉЃЎ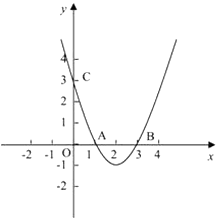
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§ЙиЯЕЪН.
ЃЈ2ЃЉНЋy=ax2+bx+cЛЏГЩy=aЃЈxЉmЃЉ2+kЕФаЮЪН(ЧыжБНгаДГіД№АИ).
ЃЈ3ЃЉШєЕуDЃЈ3.5ЃЌmЃЉЪЧХзЮяЯпy=ax2+bx+cЩЯЕФвЛЕуЃЌЧыЧѓГіmЕФжЕЃЌВЂЧѓГіДЫЪБЁїABDЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁбO жа,PЪЧЁбOФквЛЕуЃЌЙ§ЕуPзюЖЬКЭзюГЄЕФЯвЗжБ№ЮЊ6КЭ10ЃЌдђОЙ§ЕуPЧвГЄЖШЮЊећЪ§ЕФЕФЯвЙВгаЃЈ ЃЉЬѕЁЃ
A.5
B.8
C.10
D.ЮоЪ§Ьѕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇЩњдкВйГЁЩЯРћгУШ§НЧКЏЪ§ВтСПЦьИЫABЕФИпЃЌжБЯпlЮЊЫЎЦНЕиУцЃЌСНИіЭЌбЇАб30ЁуЕФШ§НЧАхКЭСПНЧЦїАДШчЭМЫљЪОЕФЗНЪНДЙжБЗХдкЕиУцЩЯЃЌСПНЧЦїЕФСуПЬЖШЯпгыЕиУцжиКЯЃЌДЫЪБЦьИЫЖЅВПBЕФгАзгЧЁКУТфдкШ§НЧаЮАхЕФЖЅЕуDДІКЭСПНЧЦї37ЁуЕФПЬЖШCДІЃЌвбжЊШ§НЧаЮАхЕФБпDE=60РхУзЃЌСПНЧЦїЕФАыОЖr=25РхУзЃЌСПНЧЦїЕФдВаФOЕНAЕФОрРыЮЊ5УзЃЎ 
ЃЈ1ЃЉдђЁЯAOC=ЁуЃЈжБНгаДГіД№АИЃЉ
ЃЈ2ЃЉЧѓЦьИЫABЕФИпЖШЃЈОЋШЗЕН0.1УзЃЌВЮПМЪ§Онsin37ЁуЁж0.6ЃЌcos37ЁуЁж0.8ЃЌtan37ЁуЁж0.75ЃЌ ![]() Ёж1.73ЃЉ
Ёж1.73ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com