
【题目】如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )

A.(m﹣60)°B.(180﹣2m)°C.(2m﹣90)°D.(120﹣m)°
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x轴的正半轴上,顶点C的坐标为(1,![]() ).
).
(1)求图象过点B的反比例函数的解析式;
(2)求图象过点A,B的一次函数的解析式;
(3)在第一象限内,当以上所求一次函数的图象在所求反比例函数的图象下方时,请直接写出自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OBC中,边BC的垂直平分线交∠BOC的平分线于点D,连接DB,DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,求∠BDC的度数;
(2)若∠BOC=![]() ,则∠BDC= ;(直接写出结果)
,则∠BDC= ;(直接写出结果)
(3)直接写出OB,OC,OF之间的数量关系.
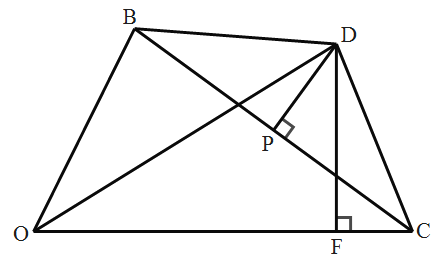
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于
,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于![]() 的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的有________.
的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的有________.
①AD是![]() 的平分线;②
的平分线;②![]() ;③点D在AB的中垂线上;④
;③点D在AB的中垂线上;④![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长为( )
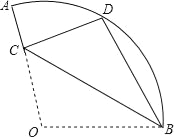
A. 2π B. 3π C. 4π D. 5π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:AE=BE;
(2)求证:FE是⊙O的切线;
(3)若FE=4,FC=2,求⊙O的半径及CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有![]() 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为![]() 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为![]() 个.
个.
![]() 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率;
![]() 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.

(1)如图1,若CE=CF,求证:DE=DF;
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点D(m,m+8)在第二象限,点B(0,n)在y轴正半轴上,作DA⊥x轴,垂足为A,已知OA比OB的值大2,四边形AOBD的面积为12.

(1)求m和n的值.
(2)如图2,C为AO的中点,DC与AB相交于点E,AF⊥BD,垂足为F,求证:AF=DE.
(3)如图3,点G在射线AD上,且GA=GB,H为GB延长线上一点,作∠HAN交y轴于点N,且∠HAN=∠HBO,求NB﹣HB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com