
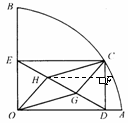
如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点。过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE。
![]() (1)求证:四边形OGCH为平行四边形;
(1)求证:四边形OGCH为平行四边形;
(2)①当点C在AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;若不存在,请说明理由;
②求![]() CD2+CH2之值。
CD2+CH2之值。
 |
(1)证明:如右图,∵CD⊥OA,CE⊥OB,
∴∠ODC=∠OEC=90°
又∵∠AOB=90°,∴四边形OECD是矩形。……(1分)
∴OD=EC,且OD//EC,∴∠ODG=∠CEH
∵DG=EH,∴△ODG≌△CEH,
∴OG=CH。
同理可证OH=CG
∴四边形OGCH为平行四边形……………………(3分)
(2)①解:线段DG的长度不变。…………………………………………………(4分)
![]() ∵点C是AB上的点,OA=6。∴OC=OA=6
∵点C是AB上的点,OA=6。∴OC=OA=6
∵四边形OECD是矩形,∴ED=OC=6………………………………………………(5分)
∵DG=GH=HE,∴DG=![]() ED=2………………………………………………………(6分)
ED=2………………………………………………………(6分)
②解:如右图,过点H作HF⊥CD于点F,
∵EC⊥CD,∴HF//EC
∴△DHF∽△DEC, ∴![]() ,∴
,∴![]() ……………………(7分)
……………………(7分)
 从而CF=CD-FD=
从而CF=CD-FD=![]() CD
CD
在Rt△CHF中,CH2=HF2+CF2=HF2+![]() CD2
CD2
在Rt△HFD中,HF2=DH2-DF2=![]() CD2………………(9分)
CD2………………(9分)
∴CH2=![]() CD2+
CD2+![]() CD2=16-
CD2=16-![]() CD2
CD2
∴![]() ……………………………………(11分)
……………………………………(11分)


科目:初中数学 来源: 题型:
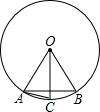 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )| A、弦AB的长等于圆内接正六边形的边长 | ||||
| B、弦AC的长等于圆内接正十二边形的边长 | ||||
C、
| ||||
| D、∠BAC=30° |
查看答案和解析>>
科目:初中数学 来源: 题型:
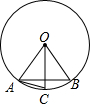 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的是( )| A、①②④ | B、①③④ | C、②③④ | D、①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:
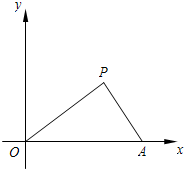 (2007•上海模拟)已知:如图,在△OAP中,OA=6,sin∠POA=
(2007•上海模拟)已知:如图,在△OAP中,OA=6,sin∠POA=| 3 |
| 5 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com