练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    对于两个代数式：①3x+1，②
    12
    x    ．我们约定一个规则：若正整数x为奇数，我们就根据①式求对应值；若正整数x为偶数，我们就根据②式求对应值．例如：给出正整数为14，先由②式求得值为7，再由①式求得值为22，…不断这样下去，最后我们将会得到一个有趣的规律．请你随意再换一个正整数试一试，用文字语言叙述这个有趣的规律：
     
    ．
    分析：随意找一个正整数，按照两个代数式进行计算，从而得到规律．
    解答：解：当x=12时，
    由题意可得：产生的结果依次为：6、3、10、5、16、8、4、2、1、4、2、1…，
    由此可以发现：任选一个正整数按此方法求值，最后结果为4、2、1循环出现．
    故答案为任选一个正整数按此方法求值，最后结果为4、2、1循环出现．
    点评：本题主要考查代数式的求值，关键是找到规律．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    24、任意写出一个数位不含0的三位数，任取三个数字中的两个，组合成所有可能的两位数（6个）．求出所有这些两位数的和，然后将它除以原三位数上的数字之和．例如对于三位数223，取其两个数字组成所有可能的两位数有：22，23，23，22，32，32．它们的和是154．三位数223各个数位上的数字之和为7，154÷7=22．再换几个数试一试，你发现了什么？运用代数式的知识说明你的发现是正确的．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

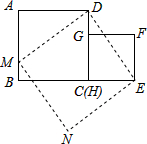    【问题提出】如何把n个正方形拼接成一个大正方形？
    为解决上面问题，我们先从最基本，最特殊的情形入手．对于边长为a的两个正方形ABCD和EFGH，如何把它们拼接成一个正方形？
    【问题解决】对于边长为a的两个正方形ABCD和EFGH，按图所示的方式摆放，在沿虚线BD，EG剪开后，可以按图中所示的移动方式拼接为图中的四边形BNED．从拼接的过程容易得到结论：
    ①四边形BNED是正方形；
    ②S正方形ABCD+S正方形EFGH=S正方形BNED．
    【类比应用】
    对于边长分别为a，b（a＞b）的两个正方形ABCD和EFGH，按图所示的方式摆放，连接DE，过点D作DM⊥DE，交AB于点M，过点M作MN⊥DM，过点E作EN⊥DE，MN与EN相交于点N．明四边形MNED是正方形，并请你用含a，b的代数式表示正方形MNED的面积；
    ②如图，将正方形ABCD和正方形EFGH沿虚线剪开后，能够拼接为正方形MNED，请简略说明你的拼接方法（类比如图，用数字表示对应的图形直接画在图中）．
    【拓广延伸】对于n（n是大于2的自然数）个任意的正方形，能否通过若干次拼接，将其拼接成为一个正方形？请简要说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    对于两个代数式：①3x+1，②数学公式．我们约定一个规则：若正整数x为奇数，我们就根据①式求对应值；若正整数x为偶数，我们就根据②式求对应值．例如：给出正整数为14，先由②式求得值为7，再由①式求得值为22，…不断这样下去，最后我们将会得到一个有趣的规律．请你随意再换一个正整数试一试，用文字语言叙述这个有趣的规律：
    ________．

    查看答案和解析>>

    科目：初中数学 来源：期中题 题型：填空题

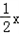    对于两个代数式：①3x+1，②．我们约定一个规则：若正整数x为奇数，我们就根据①式求对应值；若正整数x为偶数，我们就根据②式求对应值．例如：给出正整数为14，先由②式求得值为7，再由①式求得值为22，…不断这样下去，最后我们将会得到一个有趣的规律．请你随意再换一个正整数试一试，用文字语言叙述这个有趣的规律：（     ）

    查看答案和解析>>

    同步练习册答案