[题目]如图.AC与BD相交于点O.∠D=∠C.添加下列哪个条件后.仍不能使△ADO≌△BCO的是( )A. AD=BC B. AC=BD C. OD=OC D. ∠ABD=∠BAC 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，AC与BD相交于点O，∠D=∠C，添加下列哪个条件后，仍不能使△ADO≌△BCO的是（　　）

A. AD=BC B. AC=BD C. OD=OC D. ∠ABD=∠BAC

【答案】B

【解析】

由题意可知，在△ADO和△BCO中，已经有：∠D=∠C，∠AOD=∠BOC，结合各选项中添加的条件可知：

A选项中，当添加AD=BC后，结合已有条件，可由“AAS”证得△ADO≌△BCO；

B选项中，当添加AC=BD后，结合已有条件，不能证明△ADO≌△BCO；

C选项中，当添加OD=OC后，结合已有条件，可由“ASA”证得△ADO≌△BCO；

D选项中，当添加∠ABD=∠BAC后，结合已有条件，可先证得△ABD≌△BAC，从而得到AD=BC，再由“AAS”可证得△ADO≌△BCO；

故选B.

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

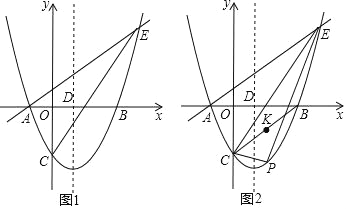
【题目】如图，在平面直角坐标系中，抛物线y=x2﹣2x﹣3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，对称轴x轴交于点D，点E（4，n）在抛物线上．

（1）求直线AE的解析式；

（2）连接CB，点K是线段CB的中点，点M是y轴上的一点，点P为直线CE下方抛物线上的一点，连接PC，PE，当△PCE的面积最大时，求KM+PM的最小值；

（3）点G是线段CE的中点，将抛物线y=x2﹣2x﹣3沿x轴正方向平移得到新抛物线y′，y′经过点D，y′的顶点为点F，在新抛物线y′的对称轴上，是否存在一点Q，使得△FGQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，⊙O的直径AB为10cm，弦BC为5cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC=PE．

（1）求AC、AD的长；

（2）试判断直线PC与⊙O的位置关系，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知△ABC中,AH⊥BC，垂足为H,若AB+BH=CH,∠ABH=80°,则∠BAC=_________ 。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，菱形的顶点与原点重合，点在轴的

正半轴上，点在反比例函数的图象上，点的坐标为．

求的值．

若将菱形向右平移，使点落在反比例函数的图象上，求菱形平移的距离．

怎样平移可以使点、同时落在第一象限的曲线上？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（2017湖北省鄂州市）小明想要测量学校食堂和食堂正前方一棵树的高度，他从食堂楼底M处出发，向前走3米到达A处，测得树顶端E的仰角为30°，他又继续走下台阶到达C处，测得树的顶端E的仰角是60°，再继续向前走到大树底D处，测得食堂楼顶N的仰角为45°．已知A点离地面的高度AB=2米，∠BCA=30°，且B、C、D三点在同一直线上．

（1）求树DE的高度；

（2）求食堂MN的高度．